Exam 18: Simplex-Based Sensitivity Analysis and Duality
Exam 1: Introduction53 Questions
Exam 2: An Introduction to Linear Programming56 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution44 Questions
Exam 4: Linear Programming Applications in Marketing, finance, and OM52 Questions
Exam 5: Advanced Linear Programming Applications39 Questions
Exam 6: Distribution and Network Models62 Questions
Exam 7: Integer Linear Programming52 Questions
Exam 8: Nonlinear Optimization Models45 Questions
Exam 9: Project Scheduling: Pertcpm60 Questions
Exam 10: Inventory Models60 Questions
Exam 11: Waiting Line Models56 Questions
Exam 12: Simulation53 Questions
Exam 13: Decision Analysis80 Questions
Exam 14: Multicriteria Decisions42 Questions
Exam 15: Time Series Analysis and Forecasting53 Questions
Exam 16: Markov Processes36 Questions
Exam 17: Linear Programming: Simplex Method45 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality32 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems39 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming41 Questions
Select questions type
Creative Kitchen Tools manufactures a wide line of gourmet cooking tools from stainless steel.For the coming production period,there is demand of 1200 for eight-quart stock pots and unlimited demand for three-quart mixing bowls and large slotted spoons.In the following model,the three variables measure the number of pots,bowls,and spoons to make.The objective function measures profit.Constraint 1 measures steel,constraint 2 measures manufacturing time,constraint 3 measures finishing time,and constraint 4 measures the stock pot demand. 
The final tableau is as follows:
The final tableau is as follows: 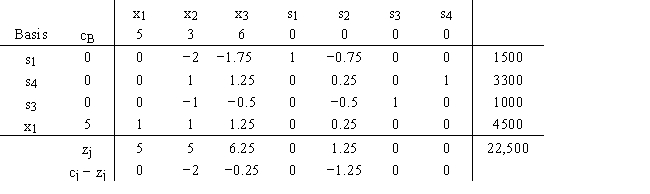
a.Calculate the range of optimality for c1,c2,and c3.
b.Calculate the range of feasibility for b1,b2,b3,and b4.
c.
Suppose that the inventory records were incorrect and the company really has only 14,000 units of steel.What effect will this have on your solution?
d.
Suppose that a cost increase will change the profit on the pots to $4.62.What effect will this have on your solution?
e.
Assume that the cost of time in production and finishing is relevant.Would you be willing to pay a $1.00 premium over the normal cost for 1000 more hours in the production department? What would this do to your solution?
a.Calculate the range of optimality for c1,c2,and c3.
b.Calculate the range of feasibility for b1,b2,b3,and b4.
c.
Suppose that the inventory records were incorrect and the company really has only 14,000 units of steel.What effect will this have on your solution?
d.
Suppose that a cost increase will change the profit on the pots to $4.62.What effect will this have on your solution?
e.
Assume that the cost of time in production and finishing is relevant.Would you be willing to pay a $1.00 premium over the normal cost for 1000 more hours in the production department? What would this do to your solution?
(Essay)
4.7/5  (43)
(43)
The dual price is the improvement in value of the optimal solution per unit increase in a constraint's right-hand-side value.
(True/False)
4.8/5  (35)
(35)
The range of feasibility indicates right-hand-side values for which
(Multiple Choice)
4.8/5  (40)
(40)
We can often avoid the process of formulating and solving a modified linear programming problem by using the range of optimality to determine whether a change in an objective function coefficient is large enough to cause a change in the optimal solution.
(True/False)
4.8/5  (33)
(33)
A linear programming problem with the objective function 3x1 + 8x2 has the optimal solution x1 = 5,x2 = 6.If c2 decreases by 2 and the range of optimality shows 5 ≤ c2 ≤ 12,the value of Z
(Multiple Choice)
4.9/5  (42)
(42)
For the following linear programming problem 
the final tableau is
the final tableau is 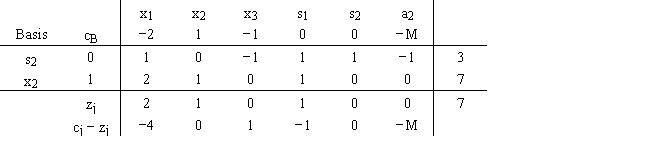
a.Find the range of optimality for c1,c2,c3,c4,c5,and c6.
b.Find the range of feasibility for b1 and b2.
a.Find the range of optimality for c1,c2,c3,c4,c5,and c6.
b.Find the range of feasibility for b1 and b2.
(Essay)
4.7/5  (31)
(31)
The range of optimality for a basic variable defines the objective function coefficient values for which that variable will remain part of the current optimal basic feasible solution.
(True/False)
4.9/5  (32)
(32)
As long as the objective function coefficient remains within the range of optimality,the variable values will not change although the value of the objective function could.
(True/False)
5.0/5  (29)
(29)
The ranges for which the right-hand-side values are valid are the same as the ranges over which the dual prices are valid.
(True/False)
4.9/5  (40)
(40)
Within the concept of duality is the original formulation of a linear programming problem known as the primal problem.
(True/False)
4.9/5  (25)
(25)
Showing 21 - 32 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)