Exam 4: Applications of the Derivative
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
The following is the graph of 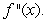 Where do the points of inflection of
Where do the points of inflection of  occur, and on which intervals is
occur, and on which intervals is  concave up?
concave up? 
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
Inflection points: B, D, F
Concave Up: [A, B], [D, F]
The following table describes the signs of the first and second derivatives of a function 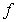 :
: 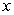 0
1
2
0
1
2 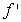 +
+
+
+
+
0
-
+
+
+
+
+
0
- 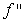 -
0
+
-
-
-
-
Which of the following is a possible graph of
-
0
+
-
-
-
-
Which of the following is a possible graph of 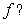
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
Find the maximum value 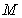 and the minimum value
and the minimum value 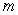 of the function in the given interval.
A)
of the function in the given interval.
A) 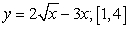 B)
B) 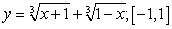
Free
(Essay)
4.9/5  (35)
(35)
Correct Answer:
A) 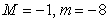 B)
B) 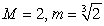
Find the maximum value 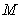 and the minimum value
and the minimum value 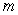 of the function in the given interval
A)
of the function in the given interval
A) 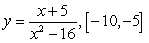 B)
B) 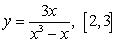
(Essay)
5.0/5  (37)
(37)
Determine the greater between 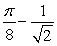 and
and 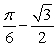 without using a calculator, by considering the function
without using a calculator, by considering the function 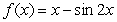 for
for 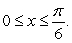
(Essay)
4.9/5  (32)
(32)
A factory produces 2000 products each month. The expenses on each product are 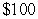 and the income from each product is
and the income from each product is 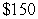 . For each additional product beyond the first 2000 products, the income for each product reduces by
. For each additional product beyond the first 2000 products, the income for each product reduces by 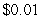 (for example, for 2001 products the income from each product is
(for example, for 2001 products the income from each product is 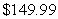 ).
A) Find the profit in a month for which
).
A) Find the profit in a month for which 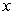 additional product are produced.
B) How many additional products should be produced to obtain maximum profit in a month?
additional product are produced.
B) How many additional products should be produced to obtain maximum profit in a month?
(Essay)
4.8/5  (32)
(32)
Given 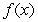 such that
such that 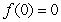 and
and 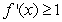 for all
for all 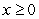 , is
, is 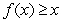 for all
for all 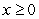 ?
(Hint: Use the MVT.)
?
(Hint: Use the MVT.)
(Multiple Choice)
4.8/5  (43)
(43)
The following table describes the signs of the first and second derivatives of a function 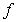 :
:  0
1
2
0
1
2 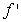
 0
0 

 0
0 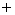
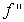
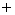 0
0  0
0 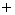
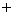
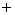 If
If 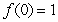 , sketch a possible graph of
, sketch a possible graph of 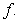
(Essay)
4.9/5  (23)
(23)
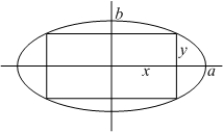
Find the dimensions and the perimeter of the rectangle with maximum perimeter, inscribed in the ellipse 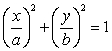 .
. 
(Essay)
4.9/5  (30)
(30)
A right circular cylinder is to be constructed with a volume of 400 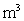 . The material used to build the top and base of the cylinder costs
. The material used to build the top and base of the cylinder costs 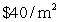 . The material for the remainder of the cylinder costs
. The material for the remainder of the cylinder costs 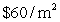 . Find the radius value which will minimize the material cost of constructing the cylinder.
. Find the radius value which will minimize the material cost of constructing the cylinder.
(Essay)
4.7/5  (30)
(30)
Estimate the roots of the equation 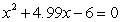 to three decimal places using the linear approximation for
to three decimal places using the linear approximation for 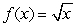 .
.
(Essay)
4.8/5  (31)
(31)
Show that the equation 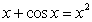 has a solution in the interval
has a solution in the interval 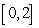 and use Newton's Method to approximate it to within an error of at most
and use Newton's Method to approximate it to within an error of at most 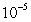 .
.
(Short Answer)
4.8/5  (29)
(29)
A ball produced on an assembly line is supposed to have a volume of 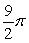
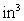 . Use linearization to estimate the maximum allowable error in the radius
. Use linearization to estimate the maximum allowable error in the radius 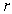 if the volume of the sphere must have an error of less than
if the volume of the sphere must have an error of less than 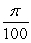
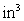 .
.
(Essay)
4.9/5  (26)
(26)
Find the maximum value 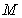 and the minimum value
and the minimum value 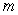 of the function in the given interval or in its natural domain
A)
of the function in the given interval or in its natural domain
A) 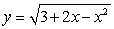 B)
B) 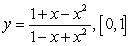 C)
C) 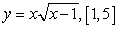
(Essay)
4.8/5  (44)
(44)
A producer can sell 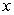 instruments per week for
instruments per week for 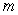 dollars each, where
dollars each, where 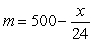 . His cost for producing
. His cost for producing 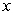 instruments is
instruments is 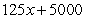 dollars.
Find the amount of instruments that should be produced in a week to obtain maximum profit.
dollars.
Find the amount of instruments that should be produced in a week to obtain maximum profit.
(Essay)
4.9/5  (27)
(27)
A cylinder of radius 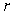 and height
and height 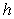 has surface area
has surface area 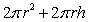 and volume
and volume 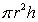 . Find the dimensions of a cylinder with volume
. Find the dimensions of a cylinder with volume 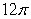 and minimal surface area.
and minimal surface area.
(Essay)
4.9/5  (40)
(40)
True or False: Let 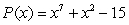 . By Rolle's Theorem,
. By Rolle's Theorem, 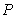 has at most 3 real roots.
has at most 3 real roots.
(True/False)
4.9/5  (30)
(30)
The following function has a local extremum at a point in the interval 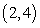 :
:
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)