Exam 15: Differentiation in Several Variables
Exam 1: Precalculus Review74 Questions
Exam 2: Limits97 Questions
Exam 3: Differentiation81 Questions
Exam 4: Applications of the Derivative77 Questions
Exam 5: The Integral82 Questions
Exam 6: Applications of the Integral80 Questions
Exam 7: Exponential Functions106 Questions
Exam 8: Techniques of Integration101 Questions
Exam 9: Further Applications of the Integral and Taylor Polynomials100 Questions
Exam 10: Introduction to Differential Equations73 Questions
Exam 11: Infinite Series95 Questions
Exam 12: Parametric Equations, Polar Coordinates, and Conic Sections71 Questions
Exam 13: Vector Geometry96 Questions
Exam 14: Calculus of Vector-Valued Functions99 Questions
Exam 15: Differentiation in Several Variables95 Questions
Exam 16: Multiple Integration98 Questions
Exam 17: Line and Surface Integrals92 Questions
Exam 18: Fundamental Theorems of Vector Analysis91 Questions
Select questions type
Given that 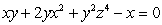 , compute the partial derivatives
, compute the partial derivatives 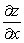 ,
, 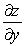 , and
, and 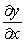 .
.
Free
(Essay)
4.9/5  (33)
(33)
Correct Answer:
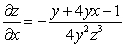 ,
, 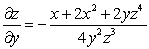 ,
, 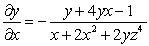
Find the global extrema of 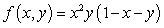 on the unit square
on the unit square 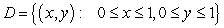 .
.
Free
(Essay)
4.7/5  (35)
(35)
Correct Answer:
Global minimum: 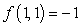 Global maximum:
Global maximum: 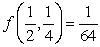
Find the linearization of 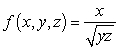 at the point
at the point 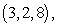 and use it to approximate
and use it to approximate 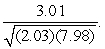
Free
(Essay)
4.7/5  (36)
(36)
Correct Answer:
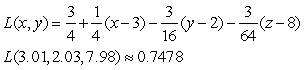
The plane 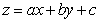 best fits the points
best fits the points 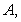
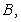
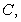 and
and 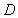 if the sum of
if the sum of 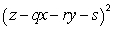 at these points is minimized by
at these points is minimized by 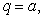
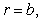 and
and 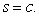 Find the plane that best fits the points
Find the plane that best fits the points 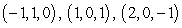 , and
, and 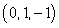 .
.
(Essay)
4.7/5  (40)
(40)
Find the distance from the origin to the surface 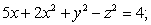 that is, the minimum distance between the origin and a point on the surface.
that is, the minimum distance between the origin and a point on the surface.
(Essay)
4.7/5  (41)
(41)
Find the critical points of the function 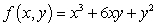 , and analyze them using the second derivative test.
, and analyze them using the second derivative test.
(Essay)
4.7/5  (33)
(33)
Find the distance from the origin to the surface 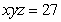 ; that is, the minimum distance between the origin and a point on the surface.
; that is, the minimum distance between the origin and a point on the surface.
(Essay)
4.8/5  (38)
(38)
Let 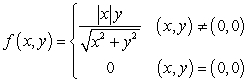 .
A) Is
.
A) Is 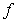 differentiable at the origin?
B) Does
differentiable at the origin?
B) Does 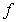 have a tangent plane at the origin? If so, find its equation.
have a tangent plane at the origin? If so, find its equation.
(Essay)
4.7/5  (38)
(38)
The temperature at 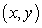 on a metal plate is
on a metal plate is 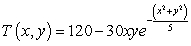 .
A) A heat seeking insect is placed at the point
.
A) A heat seeking insect is placed at the point 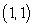 . In what direction should it move in order to feel the greatest increase in heat? What is the rate of change of temperature in this direction?
B) The insect is placed at the point
. In what direction should it move in order to feel the greatest increase in heat? What is the rate of change of temperature in this direction?
B) The insect is placed at the point 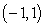 and is very hot. In what direction should it move in order to cool off at the fastest rate?
What is the rate of change of temperature in this direction?
and is very hot. In what direction should it move in order to cool off at the fastest rate?
What is the rate of change of temperature in this direction?
(Essay)
4.9/5  (35)
(35)
Let 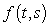 be differentiable, and let
be differentiable, and let 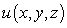 be the function
be the function 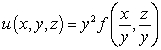 .
Compute the partial derivatives
.
Compute the partial derivatives 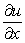 ,
, 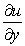 , and
, and 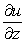 .
.
(Essay)
4.9/5  (36)
(36)
Which of the following functions satisfies the differential equation 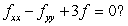
(Multiple Choice)
4.7/5  (37)
(37)
Let 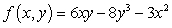 .
Find the critical points of
.
Find the critical points of 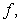 and analyze them using the second derivatives.
and analyze them using the second derivatives.
(Essay)
5.0/5  (40)
(40)
Find the critical points of 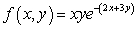 for
for 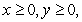 and analyze them using the second derivative test.
and analyze them using the second derivative test.
(Essay)
4.8/5  (33)
(33)
Showing 1 - 20 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)