Exam 4: Applications of the Derivative
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
A certain producer determines that his cost function is 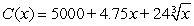 . Determine the average cost of producing 1500 units. Round answer to the nearest penny.
. Determine the average cost of producing 1500 units. Round answer to the nearest penny.
(Multiple Choice)
4.7/5  (34)
(34)
Newton's method fails for the given initial guess. Explain why the method fails and, if possible, find a root by correcting the problem. Round to four decimal places, if necessary. 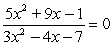 , x0 = -1
, x0 = -1
(Multiple Choice)
4.7/5  (45)
(45)
Find the intervals where the function is increasing and decreasing on the specified interval. Use this information to determine all local extrema. 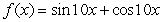 on
on 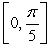
(Essay)
4.9/5  (34)
(34)
Determine the following significant features of 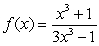 , approximating if necessary, and sketch the graph.
a). intercepts b). asymptotes
c). extrema d). inflection points
, approximating if necessary, and sketch the graph.
a). intercepts b). asymptotes
c). extrema d). inflection points 
(Essay)
4.8/5  (33)
(33)
Oil spills out of a tanker at the rate of 145 gallons per minute. The oil spreads in a circle with a thickness of 1/4 inch. Given that 1 ft3 equals 7.5 gallons, determine the rate at which the radius of the spill is increasing when the radius reaches 90 feet.
(Multiple Choice)
4.8/5  (43)
(43)
Determine the intervals where 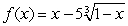 is concave up and concave down. Round answers to nearest hundredth.
is concave up and concave down. Round answers to nearest hundredth.
(Multiple Choice)
4.9/5  (37)
(37)
Using the critical numbers of 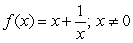 , use the Second Derivative Test to determine all local extrema.
, use the Second Derivative Test to determine all local extrema.
(Multiple Choice)
4.9/5  (36)
(36)
A person in a rowboat 2 miles from the nearest point on a straight shoreline wishes to reach his house which is 6 miles farther down the shore. If he can row at a rate of 6 miles per hour and run at a rate of 10 miles per hour, what is the minimum amount of time (in minutes) it will take him to get home? 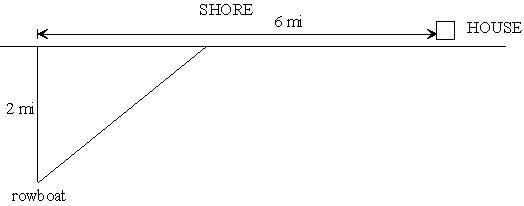
(Multiple Choice)
4.8/5  (32)
(32)
A ladder 36 feet long is leaning against a vertical wall. If the bottom of the ladder is pulled away from the base of the building at a rate of 3 ft/sec, how fast is the top of the ladder sliding down the wall when it is 28 feet above the ground? Round answer to nearest tenth.
(Multiple Choice)
4.9/5  (38)
(38)
Approximate 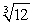 accurate to 3 decimal places using Newton's method. State the function used.
accurate to 3 decimal places using Newton's method. State the function used.
(Multiple Choice)
4.7/5  (28)
(28)
Suppose that the body temperature 30 minutes after receiving x mg of a drug is given by 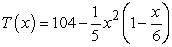 for
for  . The absolute value of the derivative,
. The absolute value of the derivative, 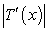 , is defined as the sensitivity of the body to the drug dosage. Find the dosage that maximizes sensitivity.
, is defined as the sensitivity of the body to the drug dosage. Find the dosage that maximizes sensitivity.
(Multiple Choice)
4.8/5  (38)
(38)
Determine the following significant features by hand and sketch the graph of 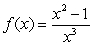 .
a). intercepts
b). asymptotes
c). extrema
d). inflection points
.
a). intercepts
b). asymptotes
c). extrema
d). inflection points 
(Essay)
4.8/5  (44)
(44)
A rectangle has its two bottom corners lying on the x-axis and the two top corners on the parabola 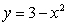 , where
, where 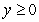 . If the area of the rectangle is to be maximized, then what are its dimensions?
. If the area of the rectangle is to be maximized, then what are its dimensions?
(Multiple Choice)
4.9/5  (44)
(44)
Showing 21 - 40 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)