Exam 4: Applications of the Derivative
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
If the concentration of a chemical changes according to the equation 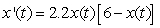 , find the concentration
, find the concentration 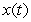 for which the reaction rate is a maximum. Round answer to nearest hundredth.
for which the reaction rate is a maximum. Round answer to nearest hundredth.
(Multiple Choice)
4.9/5  (37)
(37)
Determine, by hand, all critical numbers of 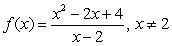 and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
(Multiple Choice)
4.9/5  (41)
(41)
Estimate the intervals where the function shown below is concave up and/or concave down. 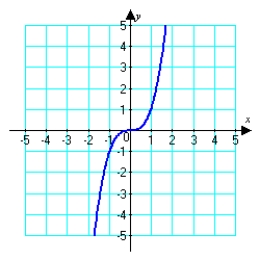
(Multiple Choice)
4.7/5  (36)
(36)
A herd of ninety-nine antelope is released onto a small game reserve so that their reproductive habits can be studied. In the beginning the population of the herd increases rapidly in size but eventually slows due to a dwindling food supply. Suppose the population of antelope after t years is given by the function 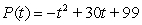 where
where 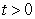 . Determine when the population begins to decline.
. Determine when the population begins to decline.
(Multiple Choice)
4.9/5  (33)
(33)
Suppose a snowball melts in such a way that it maintains a spherical shape. If the radius is decreasing at a rate of 0.75 cm per hour when the radius is 10 cm, how fast is the volume of the snowball decreasing at that instant?
(Multiple Choice)
4.8/5  (33)
(33)
Using Newton's method, approximate the root of the following equation to at least six-digit accuracy. x3 + x2 - 3x + 5 = 0
(Multiple Choice)
4.9/5  (42)
(42)
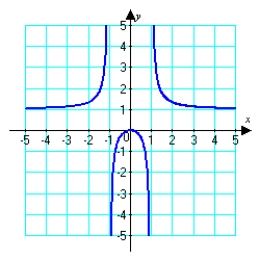
Given the graph of 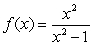 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval 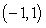 .
. 
(Multiple Choice)
4.8/5  (31)
(31)
Find (by hand) all critical numbers and use the First Derivative Test to classify each as the location of a local maximum, local minimum or neither. y = x4/3 - 8x1/3 - 6
(Multiple Choice)
4.8/5  (30)
(30)
Given 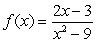 determine if the critical number
determine if the critical number 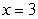 represents a local maximum, local minimum or neither.
represents a local maximum, local minimum or neither.
(Multiple Choice)
4.8/5  (48)
(48)
A certain company estimates that it can sell f(x)-thousand video game consoles at the price of $x as given in the table.  Use a linear approximation to estimate the number of consoles that can be sold at $62.
Use a linear approximation to estimate the number of consoles that can be sold at $62.
(Multiple Choice)
4.7/5  (36)
(36)
Find the absolute extrema of the given function on the indicated interval. 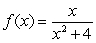 on
on 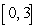
(Multiple Choice)
4.8/5  (38)
(38)
Given 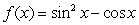 , on the interval
, on the interval 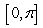 , determine if the critical number
, determine if the critical number 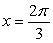 represents a local maximum, local minimum or neither.
represents a local maximum, local minimum or neither.
(Multiple Choice)
4.8/5  (38)
(38)
Find all critical numbers by hand. f (x) = x4/3 + 4x1/3 + 24x-2/3
(Multiple Choice)
4.8/5  (37)
(37)
Determine, by hand, all critical numbers of 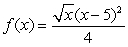 and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
(Multiple Choice)
4.8/5  (39)
(39)
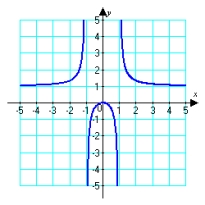
Given the graph of 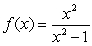 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval 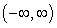 .
. 
(Multiple Choice)
4.8/5  (42)
(42)
Suppose that at the price 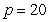 dollars the demand for a product is inelastic. If the price is increased, what will happen to revenue?
dollars the demand for a product is inelastic. If the price is increased, what will happen to revenue?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 101 - 118 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)