Exam 17: Second Order Differential Equations
Exam 1: Preliminaries101 Questions
Exam 2: Limits and Continuity105 Questions
Exam 3: Differentiation116 Questions
Exam 4: Applications of the Derivative118 Questions
Exam 5: Integration129 Questions
Exam 6: Applications of the Definite Integral85 Questions
Exam 7: Exponentials, Logarithms and Other Transcendental Functions66 Questions
Exam 8: Integration Techniques123 Questions
Exam 9: First-Order Differential Equations72 Questions
Exam 10: Infinite Series111 Questions
Exam 11: Parametric Equations and Polar Coordinates129 Questions
Exam 12: Vectors and the Geometry of Space107 Questions
Exam 13: Vector-Valued Functions103 Questions
Exam 14: Functions of Several Variables and Partial Differentiation112 Questions
Exam 15: Multiple Integrals92 Questions
Exam 16: Vector Calculus67 Questions
Exam 17: Second Order Differential Equations38 Questions
Select questions type
Find the recurrence relation for the general power series solution 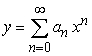 to the second order equation
to the second order equation 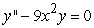 .
.
(Multiple Choice)
4.9/5  (38)
(38)
A 0.15 kg mass hangs on a spring with a 2 N m-1 force constant and its motion is damped proportional to its velocity with proportionality constant 0.4 kg s-1. If the system is subjected to an external variable-frequency vibration described as 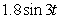 newtons, what will be the amplitude of the steady-state oscillation?
newtons, what will be the amplitude of the steady-state oscillation?
(Multiple Choice)
4.9/5  (34)
(34)
Determine the form of a particular solution of the equation. 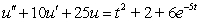
(Multiple Choice)
4.7/5  (41)
(41)
Identify the general solution of the the differential equation 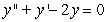 .
.
(Multiple Choice)
4.8/5  (36)
(36)
A second order differential equation can be arranged to the form 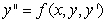 , and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is
, and one can find the third and higher derivatives of y by simply differentiating this equation. Since a Taylor-series expansion of a function y(x) is 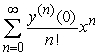 , one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation
, one can differentiate the rearranged second order differential equation to evaluate coefficients in the Taylor polynomial, if one is either given or can solve for the initial condition y(0) and y'(0). What is the coefficient of x4 in the Taylor polynomial expansion of the solution to the equation 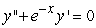 if the initial conditions are
if the initial conditions are 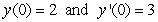 ?
?
(Multiple Choice)
4.9/5  (41)
(41)
Identify the form of a particular solution to the equation 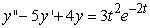 .
.
(Multiple Choice)
4.8/5  (32)
(32)
A certain spring is at rest when stretched 0.098 m by a 2.0 kg mass. Which function describes the motion of the mass if it is pulled down 0.25 m and released without imparting any initial velocity at time t = 0? Other helpful information: the motion is not damped; use 9.8 m s-2 as the acceleration due to gravity; and consider the zero position to be the rest position of the spring with the mass attached, and downward motion defines the positive x direction.
(Multiple Choice)
4.7/5  (35)
(35)
A series circuit has a 0.25 henry inductor, a 340 ohm resistor, and a 0.000009 farad capacitor. There is an initial charge of 0.000004 coulombs, there is no initial current, and there is an applied voltage which is described as 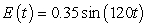 . Identify the amplitude of the steady-state solution.
. Identify the amplitude of the steady-state solution.
(Multiple Choice)
4.8/5  (35)
(35)
A spring is stretched 2 cm by a 1-kg mass. The mass is set in motion from its equilibrium position with an upward velocity of 4 m/s. The damping constant equals 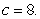 Find an equation for the position of the mass at any time t.
Find an equation for the position of the mass at any time t.
(Essay)
4.8/5  (31)
(31)
A series circuit has a 0.15 henry inductor, a 490 ohm resistor, and a 0.000004 farad capacitor. There is an applied voltage which is described as 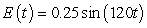 . Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
. Identify the general solution to the differential equation that describes the charge on the capacitor as a function of time.
(Multiple Choice)
4.8/5  (37)
(37)
Identify the general solution of the the differential equation 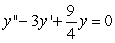 .
.
(Multiple Choice)
4.8/5  (38)
(38)
Suppose that the charge in a circuit satisfies the equation 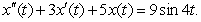 Find the gain of the circuit.
Find the gain of the circuit.
(Multiple Choice)
4.8/5  (27)
(27)
Find the recurrence relation for the general power series solution 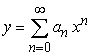 to the second order equation
to the second order equation 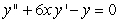 .
.
(Multiple Choice)
4.8/5  (38)
(38)
A series circuit has an 0.3 henry inductor, a 300 ohm resistor, and a 10-3 farad capacitor. The initial charge on the capacitor is 10-7 coulombs, and there is no initial current nor applied voltage. Identify the function that describes the charge on the capacitor as a function of time.
(Multiple Choice)
4.7/5  (40)
(40)
Identify the radius of convergence of the power series solutions about x = 0 of 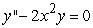 .
.
(Multiple Choice)
4.8/5  (47)
(47)
Showing 21 - 38 of 38
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)