Exam 10: Parametric Equations and Polar Coordinates
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Find the area of the indicated region. Round to the nearest ten-thousandth. Inner loop of 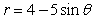
(Multiple Choice)
4.8/5  (28)
(28)
Find the speed of the object each time it crosses the x-axis. Show all your work. 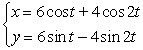
(Essay)
4.9/5  (35)
(35)
Find all slopes of the curve at the given point. [It may be helpful to graph the curve.] ![Find all slopes of the curve at the given point. [It may be helpful to graph the curve.]](https://storage.examlex.com/TB2342/11eaa948_ccc5_6799_84bc_875017297f25_TB2342_00.jpg)
(Multiple Choice)
4.9/5  (36)
(36)
Use a graphing utility to graph the conic section with focus (0, 0) and the given directrix and eccentricity. Use a window size of [-3, 3] by [-3, 3]. Directrix x = 2, e = 1
(Multiple Choice)
4.8/5  (39)
(39)
Identify a range of values of 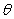 that produces one copy of the graph.
that produces one copy of the graph. 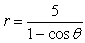
(Multiple Choice)
4.8/5  (43)
(43)
For the given parametric equations, find a corresponding x-y equation for the curve. 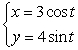
(Multiple Choice)
4.8/5  (44)
(44)
For the given parametric equations, find a corresponding x-y equation for the curve. 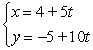
(Multiple Choice)
4.9/5  (33)
(33)
Find a polar equation for the conic section with focus (0, 0) and the given directrix and eccentricity. Directrix x = -2, e = 4
(Multiple Choice)
4.8/5  (37)
(37)
The time required for a skier, initially at rest, to ski from point A to point B on an inclined plane (where B is not directly downhill from
A ) 5.4802k
(Multiple Choice)
4.8/5  (39)
(39)
The orbits of the planets can be modeled easily by assuming i). that the sun is a perfect sphere and ii). that each planet is influenced only by the gravitational field of the sun (that is, each planet is unperturbed by gravitational forces from other planets, distant stars, etc.). According to Newton's (classical) theory of gravity, these assumptions result in elliptical planetary orbits with the sun at one focus. That is, the orbit can be described by the polar equation 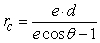 . However, according to Einstein's (relativistic) theory of gravitation, the orbits are more accurately described by
. However, according to Einstein's (relativistic) theory of gravitation, the orbits are more accurately described by 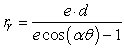 , where
, where 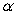 is a constant such that
is a constant such that 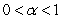 . Describe how the inclusion of the factor
. Describe how the inclusion of the factor 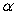 affects the orbit. That is, compare the classical orbit to the relativistic orbit. How do they differ? Draw figures that summarize the differences in the classical and relativistic orbits.
affects the orbit. That is, compare the classical orbit to the relativistic orbit. How do they differ? Draw figures that summarize the differences in the classical and relativistic orbits.
(Essay)
4.8/5  (36)
(36)
Parametric equations for the position of an object are given. Find the object's velocity and speed at the given time. 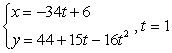
(Multiple Choice)
4.7/5  (28)
(28)
Find all polar coordinate representations of the given rectangular point. 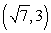
(Multiple Choice)
4.9/5  (35)
(35)
Compute the surface area of the surface obtained by revolving the given curve about the indicated axis. 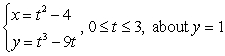
(Multiple Choice)
4.8/5  (43)
(43)
Find parametric equations describing the given curve.
The line segment from 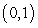 to
to 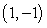
(Essay)
4.8/5  (40)
(40)
Find a polar equation corresponding to the given rectangular equation. 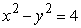
(Multiple Choice)
4.7/5  (42)
(42)
Showing 21 - 40 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)