Exam 4: Applications of the Derivative
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Bubba, a farmer, wants to fence-in a three-sided area next to his barn, using the side of the barn as the fourth side of the rectangle. He also wants to divide this rectangular area into three identical pens (see figure below). If Bubba has 104 feet of available fencing, then each pen will have what dimensions in order to maximize its area? Round dimensions to nearest tenth. 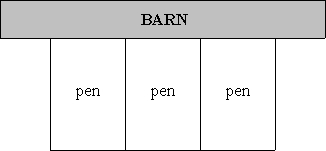
(Multiple Choice)
4.8/5  (32)
(32)
Determine, by hand, all critical numbers of 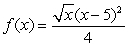 and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
(Multiple Choice)
4.9/5  (33)
(33)
A point 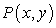 moves on the graph of the equation
moves on the graph of the equation 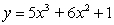 so that the x-coordinate changes at a rate of 2 units per second. How fast is the y-coordinate changing at the point
so that the x-coordinate changes at a rate of 2 units per second. How fast is the y-coordinate changing at the point 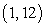
(Multiple Choice)
4.7/5  (36)
(36)
Suppose a snowball melts in such a way that it maintains a spherical shape. If the radius is decreasing at a rate of 1.75 cm per hour when the radius is 6 cm, how fast is the volume of the snowball decreasing at that instant?
(Multiple Choice)
4.7/5  (31)
(31)
Determine, by hand, all critical numbers of 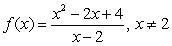 and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
(Multiple Choice)
4.9/5  (33)
(33)
Suppose the size of a particular animal's pupils expand and contract depending on the amount of light available. Let 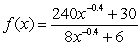 be the size in mm of the pupils at light intensity x. Find the smallest possible size of the pupils by finding
be the size in mm of the pupils at light intensity x. Find the smallest possible size of the pupils by finding 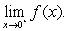
(Multiple Choice)
4.9/5  (35)
(35)
Using the critical numbers of 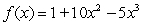 , use the Second Derivative Test to determine all local extrema.
, use the Second Derivative Test to determine all local extrema.
(Essay)
4.7/5  (41)
(41)
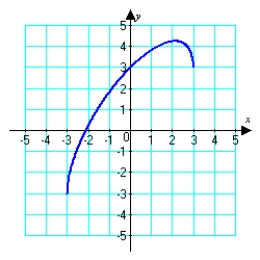
Given the graph of 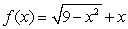 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval 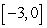 .
. 
(Multiple Choice)
4.8/5  (29)
(29)
Find the intervals where the function is increasing and decreasing on the specified interval. Use this information to determine all local extrema. 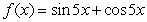 on
on 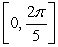
(Essay)
4.9/5  (40)
(40)
A company's revenue for selling x (thousand) items is given by 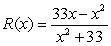 in millions of dollars. Find the value of x (rounded to the nearest item) that maximizes the revenue and find the maximum revenue (rounded to the nearest dollar).
in millions of dollars. Find the value of x (rounded to the nearest item) that maximizes the revenue and find the maximum revenue (rounded to the nearest dollar).
(Multiple Choice)
4.9/5  (46)
(46)
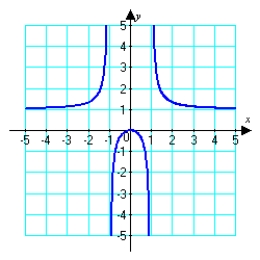
Given the graph of 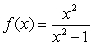 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval 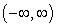 .
. 
(Multiple Choice)
4.8/5  (43)
(43)
Find the linear approximation, L(x), to f(x) at x = x0. f(x) = e7x, x0 = 0
(Multiple Choice)
4.9/5  (46)
(46)
The mass of the first x meters of a thin rod is given by the function 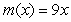 grams for
grams for 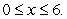 Find the linear mass density function for the rod and determine whether the composition of the rod is homogeneous or nonhomogeneous.
Find the linear mass density function for the rod and determine whether the composition of the rod is homogeneous or nonhomogeneous.
(Multiple Choice)
4.8/5  (33)
(33)
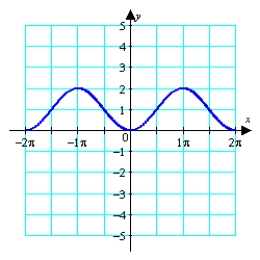
Given the graph of 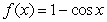 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval 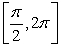 .
. 
(Multiple Choice)
4.9/5  (42)
(42)
Determine the level of production that minimizes the average cost if the cost function is 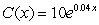 . Round answer to nearest whole number.
. Round answer to nearest whole number.
(Multiple Choice)
4.8/5  (31)
(31)
Showing 41 - 60 of 143
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)