Exam 4: Applications of the Derivative
Exam 1: Preliminaries143 Questions
Exam 2: Limits and Continuity125 Questions
Exam 3: Differentiation150 Questions
Exam 4: Applications of the Derivative143 Questions
Exam 5: Integration154 Questions
Exam 6: Applications of the Definite Integral113 Questions
Exam 7: Integration Techniques95 Questions
Exam 8: First-Order Differential Equations72 Questions
Exam 9: Infinite Series111 Questions
Exam 10: Parametric Equations and Polar Coordinates129 Questions
Exam 11: Vectors and the Geometry of Space107 Questions
Exam 12: Vector-Valued Functions103 Questions
Exam 13: Functions of Several Variables and Partial Differentiation112 Questions
Exam 14: Multiple Integrals92 Questions
Exam 15: Vector Calculus67 Questions
Exam 16: Second Order Differential Equations38 Questions
Select questions type
Sketch the graph of 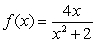 while answering the following questions.
a. What is the domain and range of
while answering the following questions.
a. What is the domain and range of 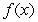 ?
b. What are the intercepts of
?
b. What are the intercepts of 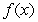 ?
c. What, if any, are the equation(s) of vertical asymototes of
?
c. What, if any, are the equation(s) of vertical asymototes of 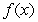 ?
d. What, if any, are the local min(s) and local max(s) of
?
d. What, if any, are the local min(s) and local max(s) of 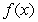 ?
e. What, if any, are the inflection point(s) of
?
e. What, if any, are the inflection point(s) of 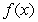 ?
f. What, if it exists, is the equation of the horizontal asymotote of
?
f. What, if it exists, is the equation of the horizontal asymotote of 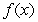 ?
? 
(Essay)
4.9/5  (37)
(37)
Determine the intervals where 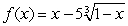 is concave up and concave down. Round answers to nearest hundredth.
is concave up and concave down. Round answers to nearest hundredth.
(Multiple Choice)
4.9/5  (40)
(40)
Using a calculator or computer, estimate the absolute extrema of 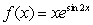 on the interval
on the interval 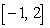 . Round answer to the nearest hundredth.
. Round answer to the nearest hundredth.
(Multiple Choice)
4.8/5  (38)
(38)
Use Newton's method with x0 = 2.3 to compute x1 and x2 without the use of a calculator.
f(x) = x3 - 3x - 5
(Essay)
4.8/5  (34)
(34)
Using Newton's method with 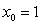 , determine the second iteration when approximating the root to at least six-digit accuracy of the following equation.
, determine the second iteration when approximating the root to at least six-digit accuracy of the following equation. 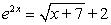
(Multiple Choice)
4.9/5  (34)
(34)
Using a calculator or computer determine all critical numbers of 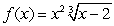 and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
and use the First Derivative Test to classify each as a local minimum, local maximum or neither.
(Multiple Choice)
4.8/5  (41)
(41)
Find the linear approximation at x = 0 to show that the following commonly used approximation is valid for "small" x. 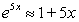
(Essay)
4.8/5  (39)
(39)
Determine the intervals where 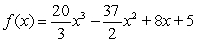 is concave up and concave down.
is concave up and concave down.
(Multiple Choice)
4.9/5  (35)
(35)
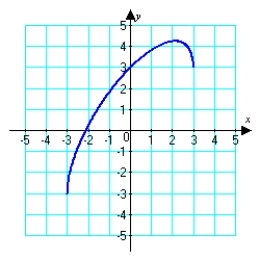
Given the graph of 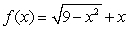 , locate the absolute extrema (if they exist) on the interval
, locate the absolute extrema (if they exist) on the interval  .
. 
(Multiple Choice)
4.7/5  (38)
(38)
Find the slant asymptote and graph the function and its asymptote on the same axes. 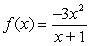
(Essay)
4.9/5  (47)
(47)
Find the linear approximation at x = 0 to show that the following commonly used approximation is valid for "small" x. 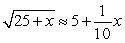
(Essay)
4.7/5  (32)
(32)
Find the intervals where the function is increasing and decreasing. Use this information to determine all local extrema. 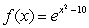
(Multiple Choice)
4.8/5  (34)
(34)
A boy standing on a cliff is watching a boat through a telescope as it approaches the base of the cliff directly below him. If the telescope is 175 feet above water level and the boat is approaching at 15 feet per second, at what rate is the angle of the telescope changing when the boat is 175 feet away?
(Multiple Choice)
4.8/5  (45)
(45)
Showing 81 - 100 of 143
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)