Exam 4: Introduction to Probability

A six-sided die is tossed 3 times. The probability of observing three ones in a row is

If P(A)  0.80, P(B)  0.65, and P(A  B)  0.78, then P(BA) 

If A and B are independent events with P(A)  0.05 and P(B)  0.65, then P(AB) 

If two events are mutually exclusive, then the probability of their intersection

The probability of an economic decline in the year 2013 is 0.23. There is a probability of 0.64 that we will elect a republican president in the year 2012. If we elect a republican president, there is a 0.35 probability of an economic decline. Let "D" represent the event of an economic decline, and "R" represent the event of election of a Republican president. a.Are "R" and "D" independent events? b.What is the probability of electing a Republican president in 2012 and an economic decline in the year 2013? c.If we experience an economic decline in the year 2013, what is the probability that a Republican president will have been elected in the year 2012? d.What is the probability of economic decline in 2013 or a Republican president elected in the year 2012 or both?

Which of the following statements is(are) always true?

If P(A)  0.85, P(A  B)  0.72, and P(A  B)  0.66, then P(B) 

In an experiment, events A and B are mutually exclusive. If P(A)  0.6, then the probability of B

Events A and B are mutually exclusive. Which of the following statements is also true?

The complement of P(A | B) is

An experiment consists of throwing two six-sided dice and observing the number of spots on the upper faces. Determine the probability that a.the sum of the spots is 3. b.each die shows four or more spots. c.the sum of the spots is not 3. d.neither a one nor a six appear on each die. e.a pair of sixes appear.f. the sum of the spots is 7.

An accounting firm has noticed that of the companies it audits, 85% show no inventory shortages, 10% show small inventory shortages and 5% show large inventory shortages. The firm has devised a new accounting test for which it believes the following probabilities hold: P(company will pass test | no shortage) = .90 P(company will pass test | small shortage) = .50 P(company will pass test | large shortage) = .20 a. If a company being audited fails this test, what is the probability of a large or small inventory shortage? b. If a company being audited passes this test, what is the probability of no inventory shortage?

If A and B are independent events with P(A)  0.4 and P(B)  0.25, then P(A  B) 

Events A and B are mutually exclusive with P(A)  0.3 and P(B)  0.2. The probability of the complement of Event B equals

A method of assigning probabilities based upon judgment is referred to as the

If a penny is tossed four times and comes up heads all four times, the probability of heads on the fifth trial is

An element of the sample space is

When the results of experimentation or historical data are used to assign probability values, the method used to assign probabilities is referred to as the

One of the basic requirements of probability is

A government agency has 6,000 employees. The employees were asked whether they preferred a four-day work week (10 hours per day), a five-day work week (8 hours per day), or flexible hours. You are given information on the employees' responses broken down by gender. 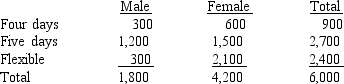a.What is the probability that a randomly selected employee is a man and is in favor of a four-day work week? b.What is the probability that a randomly selected employee is female? c.A randomly selected employee turns out to be female. Compute the probability that she is in favor of flexible hours. d.What percentage of employees is in favor of a five-day work week? e.Given that a person is in favor of flexible time, what is the probability that the person is female? f. What percentage of employees is male and in favor of a five-day work week?