Exam 4: Introduction to Probability
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Presentations116 Questions
Exam 3: Descriptive Statistics: Numerical Measures130 Questions
Exam 4: Introduction to Probability127 Questions
Exam 5: Discrete Probability Distributions146 Questions
Exam 6: Continuous Probability Distributions138 Questions
Exam 7: Sampling and Sampling Distributions123 Questions
Exam 8: Interval Estimation111 Questions
Exam 9: Hypothesis Tests117 Questions
Exam 10: Comparisons Involving Means, Experimental Design, and Analysis of Variance184 Questions
Exam 11: Comparisons Involving Proportions and a Test of Independence117 Questions
Exam 12: Simple Linear Regression107 Questions
Exam 13: Multiple Regression111 Questions
Exam 14: Statistical Methods for Quality Control72 Questions
Exam 15: Time Series Analysis and Forecastng75 Questions
Select questions type
You are given the following information on Events A, B, C, and D.
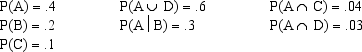 a.Compute P(D).
b.Compute P(A B).
c.Compute P(AC).
d.Compute the probability of the complement of C.
e.Are A and B mutually exclusive? Explain your answer.
f. Are A and B independent? Explain your answer.
g. Are A and C mutually exclusive? Explain your answer.
h. Are A and C independent? Explain your answer.
a.Compute P(D).
b.Compute P(A B).
c.Compute P(AC).
d.Compute the probability of the complement of C.
e.Are A and B mutually exclusive? Explain your answer.
f. Are A and B independent? Explain your answer.
g. Are A and C mutually exclusive? Explain your answer.
h. Are A and C independent? Explain your answer.
(Essay)
4.9/5  (38)
(38)
On a December day, the probability of snow is .30. The probability of a "cold" day is .50. The probability of snow and a "cold" day is .15. Are snow and "cold" weather independent events?
(Multiple Choice)
4.8/5  (46)
(46)
An experiment consists of tossing 4 coins successively. The number of sample points in this experiment is
(Multiple Choice)
4.8/5  (38)
(38)
Super Cola sales breakdown as 80% regular soda and 20% diet soda. Men purchase 60% of the regular soda, but only 30% of the diet soda. If a woman purchases Super Cola, what is the probability that it is a diet soda?
(Short Answer)
4.9/5  (41)
(41)
In a random sample of UTC students 50% indicated they are business majors, 40% engineering majors, and 10% other majors. Of the business majors, 60% were females; whereas, 30% of engineering majors were females. Finally, 20% of the other majors were female.
a.What percentage of students in this sample was female?
b.Given that a person is female, what is the probability that she is an engineering major?
(Essay)
4.7/5  (36)
(36)
An experiment consists of four outcomes with P(E1) 0.2, P(E2) 0.3, and P(E3) 0.4. The probability of outcome E4 is
(Multiple Choice)
4.7/5  (41)
(41)
A student has to take 7 more courses before she can graduate. If none of the courses are prerequisites to others, how many groups of three courses can she select for the next semester?
(Short Answer)
5.0/5  (35)
(35)
The probability assigned to each experimental outcome must be
(Multiple Choice)
4.7/5  (41)
(41)
The probability of the union of two events with nonzero probabilities
(Multiple Choice)
4.9/5  (41)
(41)
The following table shows the number of students in three different degree programs and whether they are graduate or undergraduate students:
 a.What is the probability that a randomly selected student is an undergraduate?
b.What percentage of students is engineering majors?
c.If we know that a selected student is an undergraduate, what is the probability that he or she is a business major?
d.A student is enrolled in the Arts and Sciences school. What is the probability that the student is an undergraduate student?
e.What is the probability that a randomly selected student is a graduate Business major?
a.What is the probability that a randomly selected student is an undergraduate?
b.What percentage of students is engineering majors?
c.If we know that a selected student is an undergraduate, what is the probability that he or she is a business major?
d.A student is enrolled in the Arts and Sciences school. What is the probability that the student is an undergraduate student?
e.What is the probability that a randomly selected student is a graduate Business major?
(Essay)
4.8/5  (41)
(41)
A survey of a sample of business students resulted in the following information regarding the genders of the individuals and their major.
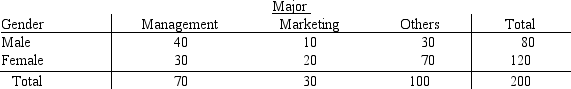 a.What is the probability of selecting an individual who is majoring in Marketing?
b.What is the probability of selecting an individual who is majoring in Management, given that the person is female?
c.Given that a person is male, what is the probability that he is majoring in Management?
d.What is the probability of selecting a male individual?
a.What is the probability of selecting an individual who is majoring in Marketing?
b.What is the probability of selecting an individual who is majoring in Management, given that the person is female?
c.Given that a person is male, what is the probability that he is majoring in Management?
d.What is the probability of selecting a male individual?
(Essay)
4.8/5  (31)
(31)
If A and B are independent events with P(A) 0.2 and P(B) 0.6, then P(A B)
(Multiple Choice)
4.8/5  (29)
(29)
Assume two events A and B are mutually exclusive and, furthermore, P(A) 0.2 and P(B) 0.4.
a.Find P(A B).
b.Find P(A B).
c.Find P(AB).
(Essay)
4.8/5  (32)
(32)
Thirty-five percent of the students who enroll in a statistics course go to the statistics laboratory on a regular basis. Past data indicates that 40% of those students who use the lab on a regular basis make a grade of B or better. On the other hand, 10% of students who do not go to the lab on a regular basis make a grade of B or better. If a particular student made an A, determine the probability that she or he used the lab on a regular basis.
(Short Answer)
4.9/5  (30)
(30)
Showing 41 - 60 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)