Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 18: Time Series and Forecasting

arrow
Exam 1: Statistics and Data100 Questionsadd course
Exam 2: Tabular and Graphical Methods123 Questionsadd course
Exam 3: Numerical Descriptive Measures151 Questionsadd course
Exam 4: Basic Probability Concepts116 Questionsadd course
Exam 5: Discrete Probability Distributions139 Questionsadd course
Exam 6: Continuous Probability Distributions128 Questionsadd course
Exam 7: Sampling and Sampling Distributions124 Questionsadd course
Exam 8: Interval Estimation123 Questionsadd course
Exam 9: Hypothesis Testing135 Questionsadd course
Exam 10: Statistical Inference Concerning Two Populations124 Questionsadd course
Exam 11: Statistical Inference Concerning Variance111 Questionsadd course
Exam 12: Chi-Square Tests120 Questionsadd course
Exam 13: Analysis of Variance58 Questionsadd course
Exam 14: Regression Analysis140 Questionsadd course
Exam 15: Inference With Regression Models124 Questionsadd course
Exam 16: Regression Models for Nonlinear Relationships115 Questionsadd course
Exam 17: Regression Models With Dummy Variables114 Questionsadd course
Exam 18: Time Series and Forecasting124 Questionsadd course
Exam 19: Returns, Index Numbers and Inflation120 Questionsadd course
Exam 20: Nonparametric Tests108 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

Under which of the following conditions is qualitative forecasting considered attractive?

(Multiple Choice)
4.8/5
(38)
Question 121

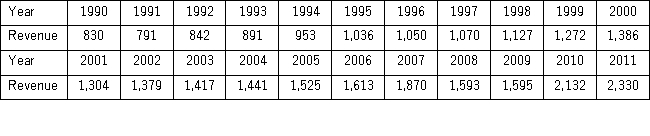The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The autoregressive models of order 1 and 2,yt = β0 + β1yt - 1 + εt,and yt = β0 + β1yt - 1 + β2yt - 2 + εt,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. 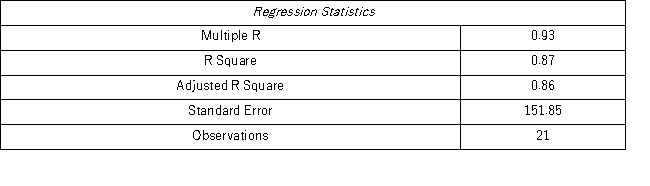Model AR(1): The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. 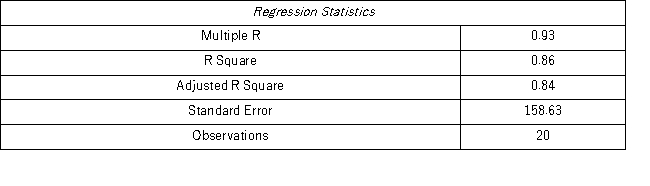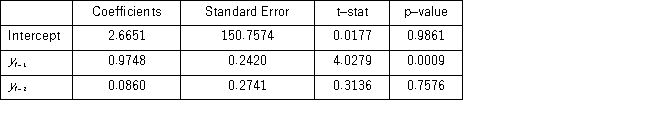The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. Model AR(2): The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. When for AR(1),H0: β0 = 0 is tested against HA: β0 ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model yt = β1yt-1 + εt might be an alternative to the AR(1)model yt = β0 + β1yt-1 + εt.Excel partial output for this simplified model is as follows: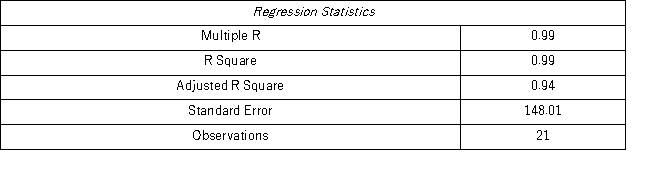 The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. The following table shows the annual revenues (in millions of dollars)of a pharmaceutical company over the period 1990-2011. The autoregressive models of order 1 and 2,y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + ε<sub>t</sub>,and y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t - </sub><sub>1</sub> + β<sub>2</sub>y<sub>t - 2</sub> + ε<sub>t</sub>,were applied on the time series to make revenue forecasts.The relevant parts of Excel regression outputs are given below. Model AR(1): Model AR(2): When for AR(1),H<sub>0</sub>: β<sub>0</sub> = 0 is tested against H<sub>A</sub>: β<sub>0</sub> ≠ 0,the p-value of this t test shown by Excel output is 0.9590.This could suggest that the model y<sub>t</sub> = β<sub>1</sub>y<sub>t</sub><sub>-1 </sub>+ ε<sub>t</sub> might be an alternative to the AR(1)model y<sub>t</sub> = β<sub>0</sub> + β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>.Excel partial output for this simplified model is as follows: Find the revenue forecast for 2012 through the use of y<sub>t</sub> = β<sub>1</sub>y<sub>t-1</sub> + ε<sub>t</sub>. Find the revenue forecast for 2012 through the use of yt = β1yt-1 + εt.

(Essay)
4.9/5
(36)
Question 122

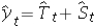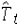When the decomposition model,yt = Tt × St × It,is applied,forecasts are made as When the decomposition model,y<sub>t</sub> = T<sub>t</sub> × S<sub>t</sub> × I<sub>t</sub>,is applied,forecasts are made as ,where represents the estimated trend for seasonally adjusted time series for period t,and is the seasonal index for period t. ,where When the decomposition model,y<sub>t</sub> = T<sub>t</sub> × S<sub>t</sub> × I<sub>t</sub>,is applied,forecasts are made as ,where represents the estimated trend for seasonally adjusted time series for period t,and is the seasonal index for period t. 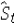represents the estimated trend for seasonally adjusted time series for period t,and When the decomposition model,y<sub>t</sub> = T<sub>t</sub> × S<sub>t</sub> × I<sub>t</sub>,is applied,forecasts are made as ,where represents the estimated trend for seasonally adjusted time series for period t,and is the seasonal index for period t. is the seasonal index for period t.

(True/False)
4.7/5
(40)
Question 123

When comparing which of the following trend models is the adjusted R2 not used?

(Multiple Choice)
5.0/5
(43)
Question 124
Showing 121 - 124 of 124
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)