Exam 9: B: large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
Refer to Swimming Average Narrative. Perform the appropriate test of hypothesis to determine whether Jessica's average time has changed. Use = 0.01.
(Essay)
4.9/5  (35)
(35)
Cable Narrative
A cable company in Ontario is thinking of offering its service in one of two cities: Guelph and Kitchener. Allegedly, there is a proportion of households in either city ready to be hooked up to the cable, but the company wants to test the claim. Accordingly, it takes a simple random sample in each city. In Guelph, 175 of 200 households say they will join. In Kitchener, 665 of 800 households say the same.
-Refer to Cable Narrative. Explain how to use the 95% confidence interval for 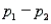 to test the appropriate hypotheses at
to test the appropriate hypotheses at 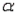 = 0.05.
= 0.05.
(Essay)
4.8/5  (39)
(39)
Soap Sales Narrative
In testing the hypotheses 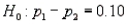 vs.
vs. 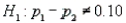 , use the following statistics:
, use the following statistics: 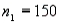 ,
, 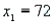 ,
, 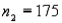 , and
, and 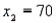 , where
, where 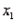 and
and 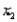 represent the number of Dial Soap sales in the two samples, respectively.
-Refer to Soap Sales Narrative. Estimate with 95% confidence the difference between the two population proportions.
represent the number of Dial Soap sales in the two samples, respectively.
-Refer to Soap Sales Narrative. Estimate with 95% confidence the difference between the two population proportions.
(Essay)
4.8/5  (37)
(37)
Swimming Average Narrative
Historically, the average time it takes Jessica to swim the 200 m butterfly is 148.4 seconds. Jessica would like to know if her average time has changed. She records her time on 50 randomly selected occasions and computes the mean to be 147.8 seconds with a standard deviation of 2.3 seconds.
-Refer to Swimming Average Narrative. Compute the power of the test if Jessica's actual mean swimming time is 147.3 seconds. Interpret the results.
(Essay)
4.7/5  (26)
(26)
Federal Votes Narrative
A Conservative party candidate in a federal election believes that 54% of Canadian voters are supporting him. His Liberal party opponentbelieves this estimate is too high.
-Refer to Federal Votes Narrative. Describe the Type I error for this .
(Essay)
4.9/5  (37)
(37)
Plant Experiments Narrative
A peony plant with red petals was crossed with another plant having streaky petals. A geneticist states that 80% of the offspring resulting from this cross will have red flowers. To test this claim, 120 seeds from this cross were collected and germinated and 84 plants had red petals.
-Refer to Plant Experiments Narrative. Calculate the test statistic and its observed significance level (p-value). Use the p-value to evaluate the statistical significance of the results at the 1% level.
(Essay)
4.9/5  (39)
(39)
Copper Pipes Narrative
A manufacturer of copper pipes must produce pipes with a diameter of precisely 5 cm. The firm's quality inspector wants to test the hypothesis that pipes of the proper size are being produced. Accordingly, a simple random sample of 100 pipes is taken from the production process. The sample mean diameter turns out to be 4.98 cm and the sample standard deviation 0.2 cm. Using a significance level of 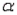 = 0.05, test the appropriate hypotheses.
-Refer to Copper Pipes Narrative. State the appropriate hypotheses.
= 0.05, test the appropriate hypotheses.
-Refer to Copper Pipes Narrative. State the appropriate hypotheses.
(Essay)
4.7/5  (30)
(30)
A new light bulb is being considered for use in an office It is decided that the new bulb will be used only if it has a mean lifetime of more than 500 hours. A random sample of 40 bulbs is selected and placed on life test. The mean and standard deviation are found to be 505 hours and 18 hours, respectively. Perform the appropriate test of hypothesis to determine whether the new bulb should be used. Use a 0.01 level of significance.
(Essay)
4.9/5  (40)
(40)
Average Childcare Costs Narrative
The public relations officer for a particular city claims the average monthly cost for childcare outside the home for a single child is $700. A potential resident is interested in whether the claim is correct. She obtains a random sample of 64 records and computes the average monthly cost of this type of childcare to be $689 with a standard deviation of $40.
-Refer to Average Childcare Costs Narrative. Perform the appropriate test of hypothesis for the potential resident using 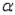 = 0.01.
= 0.01.
(Essay)
4.8/5  (38)
(38)
Swimming Average Narrative
Historically, the average time it takes Jessica to swim the 200 m butterfly is 148.4 seconds. Jessica would like to know if her average time has changed. She records her time on 50 randomly selected occasions and computes the mean to be 147.8 seconds with a standard deviation of 2.3 seconds.
-Let denote the true average delivery time of a letter from a specific carrier. For a large-sample z-test of H0: = 3 versus Ha: 3, find the p-value associated with each of the given values of the test statistic, and state whether each p-value will lead to a rejection of the null hypothesis when performing a level 0.05 test.
a. 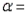 2.16
b.
2.16
b. 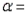 0.38
c.
0.38
c. 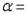 -2.81
d.
-2.81
d. 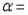 1.07
e.
1.07
e. 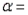 -0.68
-0.68
(Essay)
4.8/5  (32)
(32)
Copper Pipes Narrative
A manufacturer of copper pipes must produce pipes with a diameter of precisely 5 cm. The firm's quality inspector wants to test the hypothesis that pipes of the proper size are being produced. Accordingly, a simple random sample of 100 pipes is taken from the production process. The sample mean diameter turns out to be 4.98 cm and the sample standard deviation 0.2 cm. Using a significance level of 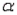 = 0.05, test the appropriate hypotheses.
-Refer to Copper Pipes Narrative. Calculate the value of the test statistic.
= 0.05, test the appropriate hypotheses.
-Refer to Copper Pipes Narrative. Calculate the value of the test statistic.
(Essay)
4.7/5  (40)
(40)
Insurance Policy Sales Narrative
Independent random samples of 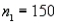 and
and 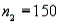 sales phone calls for an insurance policy were randomly selected from binomial populations 1 and 2, respectively. Sample 1 had 80 successful sales, and sample 2 had 88 successful sales.
-Refer to Insurance Policy Sales Narrative. Calculate the standard error of
sales phone calls for an insurance policy were randomly selected from binomial populations 1 and 2, respectively. Sample 1 had 80 successful sales, and sample 2 had 88 successful sales.
-Refer to Insurance Policy Sales Narrative. Calculate the standard error of 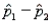 . Based on your knowledge of the standard normal distribution, is this a likely or an unlikely observation, assuming that
. Based on your knowledge of the standard normal distribution, is this a likely or an unlikely observation, assuming that 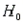 is true and the two population proportions are the same? Justify your conclusion.
is true and the two population proportions are the same? Justify your conclusion.
(Essay)
4.9/5  (32)
(32)
Life Insurance Narrative
An insurance company wants to test the hypothesis that the mean amount of life insurance held by professional men equals that held by professional women. Accordingly, two independent simple random samples are taken from appropriate professional listings of men and women. The sample of 200 men reveals a mean amount of $140,000 with a standard deviation of $26,000. The sample of 400 women shows a mean amount of $128,000 with a standard deviation of $3,000.
-Refer to Life Insurance Narrative. State the appropriate hypotheses.
(Essay)
4.9/5  (32)
(32)
A sample of size 150 is to be used to test the hypotheses H0: = 3.75 kg vs. Ha: 3.75 kg, where, is the average weight of a newborn Canadian baby. Give the appropriate rejection region associated with each of the following significance levels.
a. 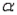 = 0.01
b.
= 0.01
b. 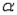 = 0.05
c.
= 0.05
c. 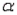 = 0.1
= 0.1
(Essay)
5.0/5  (33)
(33)
Union Contract Narrative
A union composed of several thousand employees is preparing to vote on a new contract. A random sample of 500 employees yielded 320 who planned to vote yes. It is believed that the new contract will receive more than 60% yes votes.
-Refer to Union Contract Narrative. Can we infer at the 5% significance level that the new contract will receive more than 60% yes votes? Justify your conclusion.
(Essay)
4.9/5  (35)
(35)
College Beach Volleyball Narrative
A student government representative at a local university claims that 60% of the undergraduate students favour a move from court volleyball to beach volleyball`. A random sample of 250 undergraduate students was selected and 140 students indicated they favoured a move to beach volleyball.
-Refer to College Beach Volleyball Narrative. Find the p-value for the test in the previous question.
(Essay)
4.9/5  (29)
(29)
Nuclear Weapons Freeze Narrative
A group in favour of freezing production of nuclear weapons believes that the proportion of individuals in favour of a nuclear freeze is greater for those who have seen the movie "The Day After" (population 1) than those who have not (population 2). In an attempt to verify this belief, random samples of size 500 are obtained from the populations of interest. Among those who had seen "The Day After," 228 were in favour of a freeze. For those who had not seen the movie, 196 favoured a freeze.
-Refer to Nuclear Weapons Freeze Narrative. Set up the rejection region for this test using 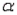 = 0.05.
= 0.05.
(Short Answer)
4.8/5  (38)
(38)
Defective Toasters Narrative
A toaster manufacturer receives large shipments of thermal switches from a supplier. A sample from each shipment is selected and tested. The manufacturer is willing to send the shipment back if the proportion of defective switches is more than 5%. Otherwise, the shipment will be kept.
-Refer to Defective Toasters Narrative. From the supplier's point of view, which error would be the more serious? Justify your answer.
(Essay)
4.8/5  (31)
(31)
Soap Sales Narrative
In testing the hypotheses 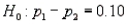 vs.
vs. 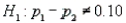 , use the following statistics:
, use the following statistics: 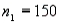 ,
, 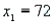 ,
, 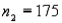 , and
, and 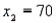 , where
, where 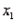 and
and 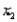 represent the number of Dial Soap sales in the two samples, respectively.
-Refer to Soap Sales Narrative. What is the p-value of the test?
represent the number of Dial Soap sales in the two samples, respectively.
-Refer to Soap Sales Narrative. What is the p-value of the test?
(Short Answer)
4.8/5  (38)
(38)
University Housing Costs Narrative Which error has more serious consequences for the student? Explain.
(Essay)
4.8/5  (34)
(34)
Showing 41 - 60 of 106
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)