Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
What is the approximate z-value you would use if you wish to construct an 85% upper confidence bound for the population proportion p?
(Multiple Choice)
4.9/5  (44)
(44)
The process of inferring the values of unknown population parameters from those of known sample statistics is called estimation.
(True/False)
4.8/5  (34)
(34)
NBA Series Narrative
A TV pollster believed that 70% of all TV households would be tuned in to Game 6 of the 2009 NBA Championship series between the LA Lakers and the Orlando Magic. A random sample of 500 TV households was selected and 365 indicated they were tuned into the game.
-Refer to NBA Series Narrative. Find a 99% confidence interval for the true proportion of TV households that tuned in to the game.
(Essay)
4.8/5  (43)
(43)
Online Time Usage Narrative
An Internet server conducted a survey of 400 of its customers and found that the average amount of time spent online was 12.5 hours per week, with a standard deviation of 5.4 hours.
-Refer to Online Time Usage Narrative. If the Internet server claimed that its users averaged 15 hours of use per week, would you agree or disagree? Explain.
(Essay)
4.9/5  (38)
(38)
A provincial job service employee wishes to estimate the mean number of people who register with the service each week. How many weeks should be sampled in order to estimate , the mean number of weekly registrants? (The employee would like the margin of error to be less than 0.5 with confidence of 0.95. Past records show the weekly standard deviation to be 2.5.) Justify your conclusion.
(Essay)
4.9/5  (38)
(38)
A point estimate is subject to sampling error and will almost always be different from the true value of the population parameter.
(True/False)
4.9/5  (46)
(46)
Number of Salon Hair Colourings Narrative
A stylist at the Hair Care Palace gathered data on the number of hair colourings given on Saturdays and on weekdays. Her results are listed below. Assume the two random samples were independently taken from normal populations.
Saturday: 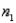 = 50 and
= 50 and 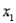 = 14
Weekday:
= 14
Weekday: 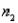 = 65 and
= 65 and 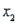 = 13
-Refer to Number of Salon Hair Colourings Narrative. Estimate the difference in the true proportions with a 99% confidence interval. Interpret this interval.
= 13
-Refer to Number of Salon Hair Colourings Narrative. Estimate the difference in the true proportions with a 99% confidence interval. Interpret this interval.
(Essay)
4.8/5  (41)
(41)
The margin of error is a half-width of an interval estimate, equal to the difference between the point estimate on the one hand and either the lower or the upper limit of the interval on the other hand.
(True/False)
4.9/5  (35)
(35)
The concept of margin of error applies directly when estimating the population mean, 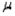 , but is not applicable when estimating the population proportion, p.
, but is not applicable when estimating the population proportion, p.
(True/False)
4.8/5  (30)
(30)
A machine produces aluminum tins used in packaging cheese. A random sample of 1000 tins was selected and 43 were found to be defective. Find a 95% upper confidence bound for the true proportion of defective tins produced by the machine. Interpret this bound.
(Essay)
5.0/5  (41)
(41)
What is the approximate z-value you would use if you wish to construct an 80% lower confidence bound for the population mean 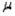 ?
?
(Multiple Choice)
4.7/5  (38)
(38)
What is the approximate z-value you would use if you wish to construct a 98% upper confidence bound for the difference between population proportions?
(Multiple Choice)
4.9/5  (30)
(30)
An estimator is unbiased if the mean of its sampling distribution is the population parameter being estimated.
(True/False)
4.7/5  (33)
(33)
A point estimate is an estimate of a population parameter, expressed as a single numerical value.
(True/False)
4.9/5  (41)
(41)
A 95% lower confidence bound (LCB) for the population mean 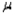 can always be constructed using the following equation: LCB =
can always be constructed using the following equation: LCB = 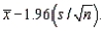
(True/False)
4.9/5  (33)
(33)
Assume that two independent random samples of sizes 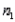 and
and 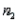 have been selected from binomial populations with parameters
have been selected from binomial populations with parameters 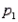 and
and 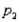 , respectively. The sampling distribution of
, respectively. The sampling distribution of 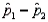 can be approximated by a normal distribution provided that
can be approximated by a normal distribution provided that 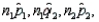 and
and 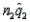 are all greater than 5.
are all greater than 5.
(True/False)
4.8/5  (33)
(33)
The maximum distance between an estimator and the true value of a parameter is called the margin of error.
(True/False)
4.8/5  (38)
(38)
A 95% confidence interval for the population proportion of professional tennis players who earn more than $2 million a year is found to be between 0.82 and 0.88. What was the approximate sample size used to obtain this information?
(Multiple Choice)
4.9/5  (37)
(37)
In order to construct a 95% confidence interval estimate for the difference between the means of two normally distributed populations, where the unknown population variances are assumed not to be equal, the following summary statistics were computed from two independent samples: 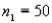 ,
, 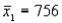 ,
, 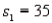 ,
, 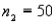 ,
, 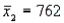 , and
, and 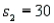 . In this case, what is the upper confidence limit?
. In this case, what is the upper confidence limit?
(Multiple Choice)
4.9/5  (40)
(40)
Lifetime of Laptop Batteries Narrative
The manufacturer of a particular battery pack for a laptop computer claims the battery pack can function for 8 hours, on average, before having to be recharged. A random sample of 36 such battery packs was selected and tested. The mean and standard deviation were found to be 6 hours and 1.8 hours, respectively.
-Refer to Lifetime of Laptop Batteries Narrative. Based on the interval in the previous question, can the manufacturer's claim be rejected? Justify your answer.
(Essay)
4.8/5  (35)
(35)
Showing 121 - 140 of 187
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)