Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
The postmaster at the Huntington Post Office would like to compare the delivery times to two different locations that are the same distance from Huntington. A random sample of letters is to be divided into two equal groups, the first to be delivered to Location A and the second to be delivered to Location B. Each letter will be delivered on a randomly selected day and the number of days for each letter to arrive at its destination is to be recorded. The measurements for both groups are expected to have a range (variability) of approximately 4 days. If the estimate of the difference in mean delivery times is desired to be correct to within 1 day, with probability equal to 0.99, how many letters must be included in each group? (Assume 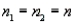 .) Justify your conclusion.
.) Justify your conclusion.
(Essay)
4.8/5  (38)
(38)
You want to estimate the difference in grade point averages between two groups of students, accurate to within 0.20 of a grade point, with confidence equal to 0.95. If the standard deviation of the grade point measurements is approximately equal to 0.5, how many students must be included in each group? (Assume that the groups will be of equal size.) Justify your conclusion.
(Essay)
4.8/5  (33)
(33)
Which of the following are possible options when estimating a population mean 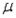 , where the population standard deviation
, where the population standard deviation 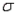 is known?
is known?
(Multiple Choice)
4.9/5  (41)
(41)
In constructing a confidence interval for a population parameter, such as 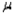 or p, the margin of error is directly dependent on the value of the point estimate.
or p, the margin of error is directly dependent on the value of the point estimate.
(True/False)
5.0/5  (41)
(41)
When two independent random samples of sizes  and
and  have been selected from populations with means
have been selected from populations with means  and
and  and variances
and variances 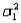 and
and  , respectively, the standard error of the sampling distribution of
, respectively, the standard error of the sampling distribution of  is found by taking the square root of the sum of the two population variances.
is found by taking the square root of the sum of the two population variances.
(True/False)
4.9/5  (40)
(40)
Which of these options is the best definition of a point estimate?
(Multiple Choice)
4.9/5  (41)
(41)
Assume that two independent random samples of sizes  and
and 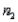 have been selected from binomial populations with parameters
have been selected from binomial populations with parameters  and
and 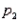 , respectively. The standard error of the sampling distribution of
, respectively. The standard error of the sampling distribution of 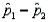 (the difference between the sample proportions) can be estimated by
(the difference between the sample proportions) can be estimated by 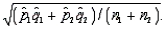
(True/False)
4.9/5  (37)
(37)
The two limits that define an interval estimate are known as confidence limits.
(True/False)
4.8/5  (35)
(35)
A questionnaire is designed to investigate attitudes about political corruption in government. The experimenter would like to survey two different groups:Conservatives and Liberals:and compare the responses to various "yes/no" questions for the two groups. The experimenter requires that the sampling error for the difference in the proportions of "yes" responses for the two groups be no more than  4 percentage points, with confidence equal to 0.95. If the two samples are both the same size, how large should the samples be? Justify your conclusion.
4 percentage points, with confidence equal to 0.95. If the two samples are both the same size, how large should the samples be? Justify your conclusion.
(Essay)
4.8/5  (41)
(41)
A study conducted by the doctors of a particular hospital involved monitoring a random sample of 75 patients. The results showed that it took an average of 3 cc of tranquillizer, with a standard deviation of 0.2 cc, to put a patient to sleep before surgery. Construct a 95% confidence interval for , the true mean amount of tranquillizer needed to put any patient to sleep.
(Essay)
4.9/5  (35)
(35)
A study was conducted to see how long Dr. Kennedy's patients had to wait before their scheduled appointments. A random sample of 33 patients showed the average waiting time was 22 minutes, with a standard deviation of 16 minutes. Construct a 99% confidence interval for , the true mean waiting time.
(Essay)
4.9/5  (40)
(40)
Independent samples of  = 400 and
= 400 and  = 400 observations were selected from binomial populations 1 and 2, and
= 400 observations were selected from binomial populations 1 and 2, and 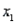 = 100 and
= 100 and  = 127 successes were observed, respectively.
a. What is the best point estimator for the difference (
= 127 successes were observed, respectively.
a. What is the best point estimator for the difference (  ) in the two binomial proportions?
b. Calculate the approximate standard error for the statistic used in (a).
c. What is the margin of error for this point estimate?
) in the two binomial proportions?
b. Calculate the approximate standard error for the statistic used in (a).
c. What is the margin of error for this point estimate?
(Essay)
4.9/5  (32)
(32)
A statistician wishes to reduce the margin of error associated with a confidence interval estimate for a population proportion p. What does she or he need to do?
(Multiple Choice)
4.9/5  (31)
(31)
Suppose a 90% confidence interval for the mean time it takes to serve a customer at a drive-in bank is 120 seconds to 220 seconds. At the 90% confidence level, there is not enough evidence to conclude that the mean service time is not 200 seconds.
(True/False)
4.7/5  (39)
(39)
A childcare agency was interested in examining the amount that families pay per child per month for childcare outside the home. A random sample of 64 families was selected and the mean and standard deviation were computed to be $675 and $80, respectively. Find a 95% upper confidence bound for the true average amount spent per child per month on childcare outside the home.
(Essay)
4.9/5  (37)
(37)
Which of the following best defines statistical estimation?
(Multiple Choice)
4.8/5  (33)
(33)
Some people claim there are health benefits in eating less meat. A health club committee reported the proportion of vegetarians in their city is 0.13. Suppose this estimate was based on a random sample of 80 people. Construct a 99% confidence interval for p, the true proportion of all vegetarians in this particular city.
(Essay)
4.7/5  (39)
(39)
A comparison between the average jail time of bank robbers and car thieves yielded the following results (in years), respectively:  = 80,
= 80, 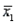 = 3.2,
= 3.2, 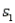 = 0.6,
= 0.6,  = 90,
= 90,  = 2.8, and
= 2.8, and 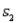 = 0.7. Estimate
= 0.7. Estimate 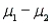 , the difference in mean years of jail time, and find the margin of error for your estimate.
, the difference in mean years of jail time, and find the margin of error for your estimate.
(Essay)
4.9/5  (43)
(43)
The unknown parameter of a population is presumed to lie at the centre of the interval that the point estimate and margin of error create.
(True/False)
4.9/5  (43)
(43)
Online Time Usage Narrative
An Internet server conducted a survey of 400 of its customers and found that the average amount of time spent online was 12.5 hours per week, with a standard deviation of 5.4 hours.
-Refer to Online Time Usage Narrative. If the distribution of the original measurements is not normal, you can still use the standard normal distribution to construct a confidence interval for  , the average online time for all users of this Internet server. Why?
, the average online time for all users of this Internet server. Why?
(Essay)
4.7/5  (35)
(35)
Showing 21 - 40 of 187
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)