Exam 5: Uncertainty and Consumer Behavior
Exam 1: Preliminaries78 Questions
Exam 2: The Basics of Supply and Demand139 Questions
Exam 3: Consumer Behavior134 Questions
Exam 4: Individual and Market Demand131 Questions
Exam 5: Uncertainty and Consumer Behavior150 Questions
Exam 6: Production125 Questions
Exam 7: The Cost of Production178 Questions
Exam 8: Profit Maximization and Competitive Supply164 Questions
Exam 9: The Analysis of Competitive Markets183 Questions
Exam 10: Market Power: Monopoly and Monopsony158 Questions
Exam 11: Pricing With Market Power130 Questions
Exam 12: Monopolistic Competition and Oligopoly120 Questions
Exam 13: Game Theory and Competitive Strategy150 Questions
Exam 14: Markets for Factor Inputs134 Questions
Exam 15: Investment, Time, and Capital Markets153 Questions
Exam 16: General Equilibrium and Economic Efficiency126 Questions
Exam 17: Markets With Asymmetric Information133 Questions
Exam 18: Externalities and Public Goods131 Questions
Exam 19: Behavioral Economics101 Questions
Select questions type
We may not be able to fully remove risk by diversification if:
(Multiple Choice)
4.8/5  (28)
(28)
The indifference curve between expected return and the standard deviation of return for a risk-averse investor:
(Multiple Choice)
4.8/5  (40)
(40)
Sam's utility of wealth function is 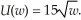 Sam owns and operates a farm. He is concerned that a flood may wipe out his crops. If there is no flood, Sam's wealth is $360,000. The probability of a flood is 1/15. If a flood does occur, Sam's wealth will fall to $160,000. Calculate the risk premium Sam is willing to pay for flood insurance.
Sam owns and operates a farm. He is concerned that a flood may wipe out his crops. If there is no flood, Sam's wealth is $360,000. The probability of a flood is 1/15. If a flood does occur, Sam's wealth will fall to $160,000. Calculate the risk premium Sam is willing to pay for flood insurance.
(Essay)
4.7/5  (35)
(35)
The information in the table below describes choices for a new doctor. The outcomes represent different macroeconomic environments, which the individual cannot predict.Table 5.3
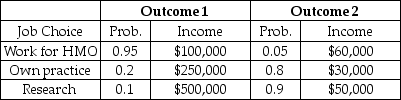 -Refer to Table 5.3. Rank the doctor's job choices in order, least risky first.
-Refer to Table 5.3. Rank the doctor's job choices in order, least risky first.
(Multiple Choice)
4.9/5  (34)
(34)
Scenario 5.2:
Randy and Samantha are shopping for new cars (one each). Randy expects to pay $15,000 with 1/5 probability and $20,000 with 4/5 probability. Samantha expects to pay $12,000 with 1/4 probability and $20,000 with 3/4 probability.
-Refer to Scenario 5.2. Which of the following is true?
(Multiple Choice)
4.8/5  (35)
(35)
Scenario 5.10:
Hillary can invest her family savings in two assets: riskless Treasury bills or a risky vacation home real estate project on an Arkansas river. The expected return on Treasury bills is 4 percent with a standard deviation of zero. The expected return on the real estate project is 30 percent with a standard deviation of 40 percent.
-Refer to Scenario 5.10. If Hillary invests 30 percent of her savings in the real estate project and remainder in Treasury bills, the standard deviation of her portfolio is:
(Multiple Choice)
4.8/5  (24)
(24)
Scenario 5.6:
Consider the information in the table below, describing choices for a new doctor. The outcomes represent different macroeconomic environments, which the individual cannot predict.
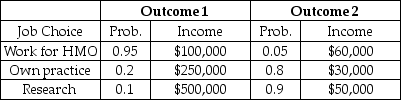 -Refer to Scenario 5.6. The utility of expected income from research is:
-Refer to Scenario 5.6. The utility of expected income from research is:
(Multiple Choice)
4.7/5  (25)
(25)
Scenario 5.1:
Aline and Sarah decide to go into business together as economic consultants. Aline believes they have a 50-50 chance of earning $200,000 a year, and that if they don't, they'll earn $0. Sarah believes they have a 75% chance of earning $100,000 and a 25% chance of earning $10,000.
-Refer to Scenario 5.1. The expected value of the undertaking,
(Multiple Choice)
4.9/5  (39)
(39)
Sandra lives in the Pacific Northwest and enjoys walking to and from work during sunny days. Her utility is sharply diminished if she must walk while it is raining. Sandra's utility function is 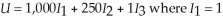 if she walks and there is no rain and
if she walks and there is no rain and 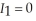 otherwise,
otherwise, 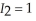 if she drives to work and
if she drives to work and 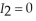 otherwise, and
otherwise, and 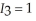 if she walks and it rains and
if she walks and it rains and 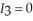 otherwise. Sandra believes that the probability of rain today is 3/10. Given her beliefs, what is her expected utility from walking to work? What is her expected utility from driving to work according to her beliefs? If Sandra maximizes her expected utility according to her beliefs, will she drive or walk to work? Sandra missed the weather report this morning that stated the true probability of rain today is 4/5. Given the weather report is accurate, what is Sandra's true expected utility from walking and driving to work? How much could Sandra increase her expected utility if she read and believed the weather report?
otherwise. Sandra believes that the probability of rain today is 3/10. Given her beliefs, what is her expected utility from walking to work? What is her expected utility from driving to work according to her beliefs? If Sandra maximizes her expected utility according to her beliefs, will she drive or walk to work? Sandra missed the weather report this morning that stated the true probability of rain today is 4/5. Given the weather report is accurate, what is Sandra's true expected utility from walking and driving to work? How much could Sandra increase her expected utility if she read and believed the weather report?
(Essay)
4.7/5  (32)
(32)
The slope of the budget line, faced by an investor deciding what percentage of her portfolio to place in a risky asset, increases when the:
(Multiple Choice)
4.8/5  (20)
(20)
Connie's utility depends upon her income. Her utility function is ![Connie's utility depends upon her income. Her utility function is She has received a prize that depends on the roll of a pair of dice. If she rolls a 3, 4, 6 or 8, she will receive $400. Otherwise she will receive $100. a. What is the expected payoff from this prize? [Hint: The probability of rolling a 3 is 1/18, the probability of rolling a 4 is 3/36, the probability of rolling a 6 is 5/36, and the probability of rolling an 8 is 5/36.] b. What is the expected utility from this prize? c. Connie is offered an alternate prize of $169 (no dice roll is required). Will she accept the alternate prize or roll the dice? d. What is the minimum payment that Connie will accept to forego the roll of the dice?](https://storage.examlex.com/TB3095/11eab6a8_3b24_f55e_9bd3_d3a779d09d58_TB3095_11.jpg) She has received a prize that depends on the roll of a pair of dice. If she rolls a 3, 4, 6 or 8, she will receive $400. Otherwise she will receive $100.
a. What is the expected payoff from this prize? [Hint: The probability of rolling a 3 is 1/18, the probability of rolling a 4 is 3/36, the probability of rolling a 6 is 5/36, and the probability of rolling an 8 is 5/36.]
b. What is the expected utility from this prize?
c. Connie is offered an alternate prize of $169 (no dice roll is required). Will she accept the alternate prize or roll the dice?
d. What is the minimum payment that Connie will accept to forego the roll of the dice?
She has received a prize that depends on the roll of a pair of dice. If she rolls a 3, 4, 6 or 8, she will receive $400. Otherwise she will receive $100.
a. What is the expected payoff from this prize? [Hint: The probability of rolling a 3 is 1/18, the probability of rolling a 4 is 3/36, the probability of rolling a 6 is 5/36, and the probability of rolling an 8 is 5/36.]
b. What is the expected utility from this prize?
c. Connie is offered an alternate prize of $169 (no dice roll is required). Will she accept the alternate prize or roll the dice?
d. What is the minimum payment that Connie will accept to forego the roll of the dice?
(Essay)
4.8/5  (34)
(34)
The risk-return indifference curves for a risk-neutral investor are:
(Multiple Choice)
4.8/5  (36)
(36)
Which of the following is NOT a generally accepted measure of the riskiness of an investment?
(Multiple Choice)
4.9/5  (44)
(44)
The relationship between income and total utility for three investors (A, B, and
C) is shown in the tables below.
A B C
Income TU Income TU Income TU
5,000 14 5,000 4 5,000 6
10,000 24 10,000 8 10,000 14
15,000 32 15,000 12 15,000 24
20,000 38 20,000 16 20,000 36
25,000 43 25,000 20 25,000 52
30,000 47 30,000 24 30,000 72
35,000 49 35,000 28 35,000 100
Each investor has been confronted with the following three investment opportunities. The first opportunity is an investment which pays $15,000 risk free. Opportunity two offers a 0.4 probability of a $25,000 payment and a 0.6 probability of paying $10,000. The final investment will either pay $35,000 with a probability of 0.25 or $5,000 with a probability of 0.75. Determine the alternative each of the above investors would choose. Provide an intuitive explanation for the differences in their choices.
(Essay)
4.8/5  (38)
(38)
Describe Larry, Judy and Carol's risk preferences. Their utility as a function of income is given as follows
Larry: 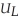 (I) = 10
(I) = 10 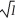 .
Judy:
.
Judy: 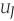 (I) = 3
(I) = 3 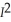 .
Carol:
.
Carol: 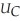 (I) = 20I.
(I) = 20I.
(Essay)
4.9/5  (33)
(33)
Last year, on advice from your sister, you bought stock in Burpsy Soda at $100/share. During the year, you collected a $2 dividend and then sold the stock for $120/share. You experienced a:
(Multiple Choice)
4.9/5  (24)
(24)
This year, on advice from your sister, you bought tobacco company stock at $50/share. During the year, you collected an $8 dividend, but due to the company's losses in medical lawsuits its stock fell to $40/share. At this point, you sell, realizing a:
(Multiple Choice)
4.9/5  (37)
(37)
Showing 61 - 80 of 150
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)