Exam 5: Uncertainty and Consumer Behavior

The information in the table below describes choices for a new doctor. The outcomes represent different macroeconomic environments, which the individual cannot predict.Table 5.3 -Refer to Table 5.3. The expected returns are highest for the physician who:

C and S Metal Company produces stainless steel pots and pans. C and S can pursue either of two distribution plans for the coming year. The firm can either produce pots and pans for sale under a discount store label or manufacture a higher quality line for specialty stores and expensive mail order catalogs. High initial setup costs along with C and S's limited capacity make it impossible for the firm to produce both lines. Profits under each plan depend upon the state of the economy. One of three conditions will prevail: growth (probability = 0.3) normal (probability = 0.5) recession (probability = 0.2) The outcome under each plan for each state of the economy is given in the table below. Figures in the table are profits measured in dollars. The probabilities for each economic condition represent crude estimates. Economic Condition Discount Line Specialty Line Growth 250,000 400,000 Normal 220,000 230,000 Recession 140,000 20,000 a. Calculate the expected value for each alternative. b. Which alternative is more risky? (Calculate the standard deviation of profits for each alternative.) c. Taking into account the importance of risk, which alternative should an investor choose?

John Smith is considering the purchase of a used car that has a bank book value of $16,000. He believes that there is a 20% chance that the car's transmission is damaged. If the transmission is damaged, the car would be worth only $12,000 to Smith. What is the expected value of the car to Smith?

Donna is considering the option of becoming a co-owner in a business. Her investment choices are to hold a risk free asset that has a return of 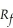and co-ownership of the business, which has a rate of return of 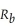and a level of risk of 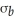. Donna's marginal rate of substitution of return for risk 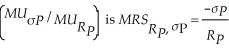where 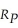is Donna's portfolio rate of return and σ_P is her optimal portfolio risk. Donna's budget constraint is given by 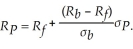Solve for Donna's optimal portfolio rate of return and risk as a function of 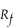, 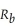and 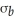. Suppose the table below lists the relevant rates of returns and risks. Use this table to determine Donna's optimal rate or return and risk. Investment Rate of Return Risk Risk Free 0.06 0 Business 0.25 0.39

An investment opportunity has two possible outcomes. The expected value of the investment opportunity is $250. One outcome yields a $100 payoff and has a probability of 0.25. What is the payoff of the other outcome?

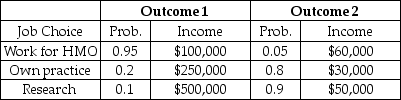
Table 5.4 -Refer to Table 5.4. If outcomes 1 and 2 are equally likely at Job A, and if at Job B the $20 outcome occurs with probability .1, and the $50 outcome occurs with probability .9, then:

An investment opportunity has two possible outcomes, and the value of the investment opportunity is $250. One outcome yields a $100 payoff and has a probability of 0.25. What is the probability of the other outcome?

Because of the relationship between an asset's real rate of return and its risk, one would expect to find all of the following, except one. Which one?

Tom Wilson is the operations manager for BiCorp, a real estate investment firm. Tom must decide if BiCorp is to invest in a strip mall in a northeast metropolitan area. If the shopping center is highly successful, after tax profits will be $100,000 per year. Moderate success would yield an annual profit of $50,000, while the project will lose $10,000 per year if it is unsuccessful. Past experience suggests that there is a 40% chance that the project will be highly successful, a 40% chance of moderate success, and a 20% probability that the project will be unsuccessful. a. Calculate the expected value and standard deviation of profit. b. The project requires an $800,000 investment. If BiCorp has an 8% opportunity cost on invested funds of similar riskiness, should the project be undertaken?

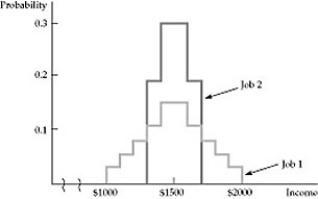Figure 5.1.2 -Refer to Figure 5.1.2 above. When Job 1 is compared to Job 2, we come to the following conclusion:

The demand curve for a particular stock at any point in time is:

The indifference curves of two investors are plotted against a single budget line. Indifference curve A is shown as tangent to the budget line at a point to the left of indifference curve B's tangency to the same line.

Scenario 5.10: Hillary can invest her family savings in two assets: riskless Treasury bills or a risky vacation home real estate project on an Arkansas river. The expected return on Treasury bills is 4 percent with a standard deviation of zero. The expected return on the real estate project is 30 percent with a standard deviation of 40 percent. -Refer to Scenario 5.10. Hillary's indifference curves showing her preferences toward risk and return can be shown in a diagram. Expected return is plotted on the vertical axis and standard deviation of return on the horizontal axis. Although her indifference curves are upward sloping and bowed downward, their slope is very gradual (they are almost horizontal). With these indifference curves Hillary will invest:

Jonathan and Roberto enjoy playing poker. Jonathan's utility as a function of winning a poker hand is 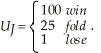Roberto's utility as a function of winning a poker hand is 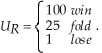Unfortunately for Jonathan, he has a habit of whistling only when he gets a full-house or better. Roberto, however, has not noticed this habit. Roberto currently has three-of-a-kind (which will lose to a full-house or better). Roberto believes that the probability Jonathan can beat his three-of-a-kind is ¹/₁₀. Roberto could choose to fold or play the hand. Calculate Roberto's expected utility according to his beliefs. Jonathan is currently whistling. How much could Roberto increase his utility by recognizing Jonathan's whistling habit?

Suppose your utility function for income that takes the form U(I) = 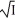, and you are considering a self-employment opportunity that may pay $10,000 per year or $40,000 per year with equal probabilities. What certain income would provide the same satisfaction as the expected utility from the self-employed position?

Blanca has her choice of either a certain income of $20,000 or a gamble with a 0.5 probability of $10,000 and a 0.5 probability of $30,000. The expected value of the gamble:

Marsha owns a boat that is harbored on the east coast of the United States. Currently, there is a hurricane that is approaching her harbor. If the hurricane strikes her harbor, her wealth will be diminished by the value of her boat, as it will be destroyed. The value of her boat is $250,000. It would cost Marsha $15,000 to move the boat to a harbor out of the path of the hurricane. Marsha's utility of wealth function is 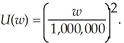Marsha's current wealth is $3 million including the value of the boat. Past evidence has influenced Marsha to believe that the hurricane will likely miss her harbor, and so she plans not to move her boat. Suppose the probability the hurricane will strike Marsha's harbor is 0.7. Calculate Marsha's expected utility given that she will not move her boat. Calculate Marsha's expected utility if she moves her boat. Which of the two options gives Marsha the highest expected utility?

Consider the following statements when answering this question: I. Without fire insurance, the expected value of home ownership for a risk averse homeowner is $W. Insurance companies are willing to sell this homeowner a policy that guarantees the homeowner a wealth of $W. II) In a neighborhood where the price of houses are identical, the probability of a fire is identical, and the value of damage done by fires is identical, the risk premium for an insurance policy that repays all the cost of the fire damage does not vary across homeowners.

The difference between the utility of expected income and expected utility from income is:

Calculate the expected value of the following game. If you win the game, your wealth will increase by 36 times your wager. If you lose, you lose your wager amount. The probability of winning is 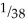Calculate the variance of the game.