Exam 13: Simulation Modeling

The time between arrivals at a drive-through window of a fast-food restaurant follows the distribution given below.The service time distribution is also given in the table below.Use the random numbers provided to simulate the activity of the first five arrivals.Assume that the window opens at 11:00 a.m.and the first arrival after this is based on the first interarrival time generated. Random numbers for arrivals: 14, 74, 27, 03 Random numbers for service times: 88, 32, 36, 24 What times does the fourth customer leave the system?

Table 13-7 A professor dutifully holds six office hours per week as dictated by an archaic policy.Demand for office hours varies wildly as reflected in this historical data. The duration of time to answer questions varies independently from the actual demand.Question duration is reflected in this table. Entries in the student demand and question duration tables that reflect a range in demand, i.e., 3-9 students per six hours or 4-9 minutes should be treated as collapsed entries in the table.Thus, a question duration of 4 minutes has a 0.05 probability, a question duration of 5 minutes also has a 0.05 probability, and so on up through 9 minutes and a 0.05 probability. This table contains random numbers for the number of students and duration of question for a 16-week period. 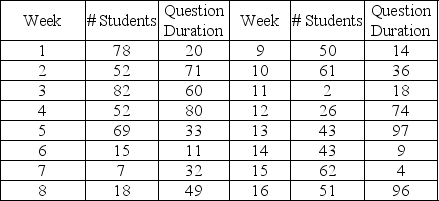Use the question duration figure as the time required to answer questions for each student that week, so if three students arrive in week seven and the average duration is ten minutes, the total time spent answering questions that week is thirty minutes. -What is the total duration of questions asked during week 3 according to the information contained in Table 13-7?

The use of simulations in competitive situations is called

Explain what is meant by operational gaming and give one example.

Table 13-3 A pharmacy is considering hiring another pharmacist to better serve customers.To help analyze this situation, records are kept to determine how many customers will arrive in any 10-minute interval.Based on 100 ten-minute intervals, the following probability distribution has been developed and random numbers assigned to each event. 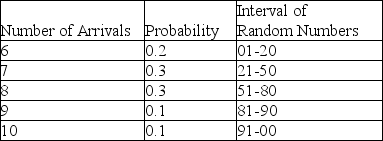-According to Table 13-3, the number of arrivals in any 10-minute period is between 6 and 10, inclusive.Suppose the next three random numbers were 18, 89, and 67, and these were used to simulate arrivals in the next three 10-minute intervals.How many customers would have arrived during this 30-minute time period?

Table 13-6 Paul prepares a variety of Creole and Cajun dishes to the delight of his diners at his restaurant in the French Quarter.Demand for crawfish etouffee follows this historical distribution: Each recipe of crawfish etouffee calls for two sticks of butter which the prep chef must buy down the block at a local grocery store.Paul would like to put in a special butter refrigerator and needs to estimate the capacity he would need if he orders twice a week from his butter supplier.He decides to simulate two weeks of this process using the historical distribution mapped to random numbers ranging from 01-00 and the random number table below. 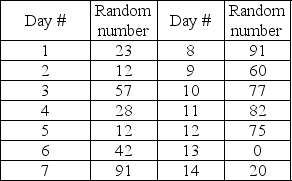-What is the total demand for butter during the first week for the scenario shown in Table 13-6?

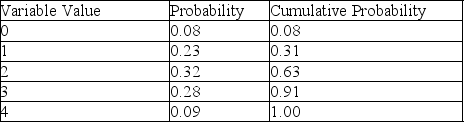
Table 13-5 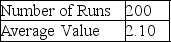-According to Table 13-5, which presents a summary of the Monte Carlo output from a simulation of 200 runs, there are 5 possible values for the variable of concern.If this variable represents the number of machine breakdowns during a day, what is the probability that the number of breakdowns is more than 4?

A professor dutifully holds six office hours per week as dictated by an archaic policy.Demand for office hours varies wildly as reflected in this historical data. The duration of time to answer questions varies independently from the actual demand.Question duration is reflected in this table. Entries in the student demand and question duration tables that reflect a range in demand, i.e., 3-9 students per six hours or 4-9 minutes should be treated as collapsed entries in the table.Thus, a question duration of 4 minutes has a 0.05 probability, a question duration of 5 minutes also has a 0.05 probability, and so on up through 9 minutes and a 0.05 probability. This table contains random numbers for the number of students and duration of question for a 16-week period. 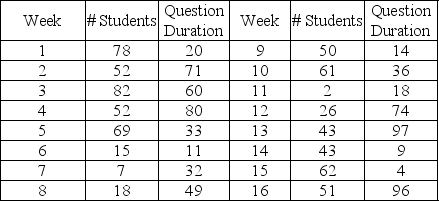Use the question duration figure as the time required to answer questions for each student that week, so if three students arrive in week seven and the average duration is ten minutes, the total time spent answering questions that week is thirty minutes. What is the number of minutes of office hour time that is used to answer questions during this simulated 16-week semester?

List the major disadvantages of simulation techniques.

One disadvantage of simulation is that it does not allow for what-if types of questions.

Validation relates to building the right model.

Table 13-7 A professor dutifully holds six office hours per week as dictated by an archaic policy.Demand for office hours varies wildly as reflected in this historical data. The duration of time to answer questions varies independently from the actual demand.Question duration is reflected in this table. Entries in the student demand and question duration tables that reflect a range in demand, i.e., 3-9 students per six hours or 4-9 minutes should be treated as collapsed entries in the table.Thus, a question duration of 4 minutes has a 0.05 probability, a question duration of 5 minutes also has a 0.05 probability, and so on up through 9 minutes and a 0.05 probability. This table contains random numbers for the number of students and duration of question for a 16-week period. Use the question duration figure as the time required to answer questions for each student that week, so if three students arrive in week seven and the average duration is ten minutes, the total time spent answering questions that week is thirty minutes. -What is the duration of questions asked during week 5 according to the information contained in Table 13-7?

A simulation that tests the number of ticket takers needed to allow fans to enter a stadium within a set period of time is one example of operational gaming.

Table 13-1 The table below represents the probability distribution for machine breakdowns in a day of operation. 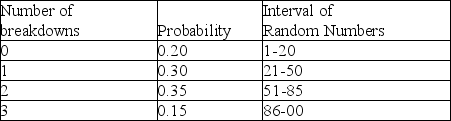-According to Table 13-1, what is the probability of at least one breakdown?

Table 13-7 A professor dutifully holds six office hours per week as dictated by an archaic policy.Demand for office hours varies wildly as reflected in this historical data. The duration of time to answer questions varies independently from the actual demand.Question duration is reflected in this table. Entries in the student demand and question duration tables that reflect a range in demand, i.e., 3-9 students per six hours or 4-9 minutes should be treated as collapsed entries in the table.Thus, a question duration of 4 minutes has a 0.05 probability, a question duration of 5 minutes also has a 0.05 probability, and so on up through 9 minutes and a 0.05 probability. This table contains random numbers for the number of students and duration of question for a 16-week period. Use the question duration figure as the time required to answer questions for each student that week, so if three students arrive in week seven and the average duration is ten minutes, the total time spent answering questions that week is thirty minutes. -Use the information in Table 13-7 to determine the range of random numbers that corresponds to a seven-minute question.

The process of determining that the computer model is internally consistent and following the logic of the conceptual model is called

If we are using a Monte Carlo simulation model, we should expect the model to produce the same results for each set of random numbers used.

In assigning random numbers in a Monte Carlo simulation

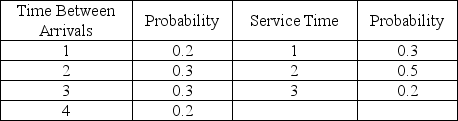
Table 13-4 A pawn shop in Arlington, Texas, has a drive-through window to better serve customers.The following tables provide information about the time between arrivals and the service times required at the window on a particularly busy day of the week.All times are in minutes. 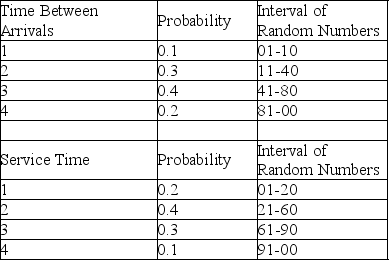The first random number generated for arrivals is used to tell when the first customer arrives after opening. -According to Table 13-4, the time between successive arrivals is 1, 2, 3, or 4 minutes.If the store opens at 8:00 a.m., and random numbers are used to generate arrivals, what time would the first customer arrive if the first random number were 02?

Explain what is meant by a Monte Carlo simulation.