Exam 40: One-Dimensional Quantum Mechanics

An electron is confined in a harmonic oscillator potential well. What is the longest wavelength of light that the electron can absorb if the net force on the electron behaves as though it has a spring constant of 74 N/m? (m_el = 9.11 × 10^-31 kg, c = 3.00 × 10⁸ m/s, 1 eV = 1.60 × 10^-19 J, h = 1.055 × 10^-34 J ∙ s, h = 6.626 × 10^-34 J ∙ s)

One fairly crude method of determining the size of a molecule is to treat the molecule as an infinite square well (a box) with an electron trapped inside, and to measure the wavelengths of emitted photons. If the photon emitted during the n = 2 to n = 1 transition has wavelength 1940 nm, what is the width of the molecule? (c = 3.00 × 10⁸ m/s, h = 6.626 × 10^-34 J ∙ s, M_el = 9.11 × 10^-31 kg)

If an atom in a crystal is acted upon by a restoring force that is directly proportional to the distance of the atom from its equilibrium position in the crystal, then it is impossible for the atom to have zero kinetic energy.

An electron in an infinite potential well (a box) makes a transition from the n = 3 level to the ground state and in so doing emits a photon of wavelength 20.9 nm. (c = 3.00 × 10⁸ m/s, h = 6.626 × 10^-34J ∙ s, m_el = 9.11 × 10^-31 kg) (a) What is the width of this well? (b) What wavelength photon would be required to excite the electron from its original level to the next higher one?

An electron is trapped in an infinite square well (a box) of width 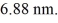Find the wavelength of photons emitted when the electron drops from the n = 5 state to the n = 1 state in this system. (c = 3.00 × 10⁸ m/s, h = 6.626 × 10^-34 J ∙ s, m_el = 9.11 × 10^-31 kg)

An electron with kinetic energy 2.80 eV encounters a potential barrier of height 4.70 eV. If the barrier width is 0.40 nm, what is the probability that the electron will tunnel through the barrier? (1 eV = 1.60 × 10^-19 J, m_el = 9.11 × 10^-31 kg, h = 1.055 × 10^-34 J ∙ s, h = 6.626 × 10^-34 J ∙ s)

A 10.0-g bouncy ball is confined in a 8.3-cm-long box (an infinite well). If we model the ball as a point particle, what is the minimum kinetic energy of the ball? (h = 6.626 × 10^-34 J ∙ s)

The atoms in a nickel crystal vibrate as harmonic oscillators with an angular frequency of 2.3 × 10¹³ rad/s. The mass of a nickel atom is 9.75 × 10^-26 kg. What is the difference in energy between adjacent vibrational energy levels of nickel? (h = 6.626 × 10^-34 J ∙ s, H = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J)

You want to have an electron in an energy level where its speed is no more than 66 m/s. What is the length of the smallest box (an infinite well) in which you can do this? (h = 6.626 × 10^-34 J ∙ s, m_el = 9.11 × 10^-31 kg)

An electron is confined in a harmonic oscillator potential well. A photon is emitted when the electron undergoes a 3→1 quantum jump. What is the wavelength of the emission if the net force on the electron behaves as though it has a spring constant of 9.6 N/m? (m_el = 9.11 × 10^-31 kg, c = 3.00 × 10⁸ m/s, 1 eV = 1.60 × 10^-19 J, h = 1.055 × 10^-34 J ∙ s, h = 6.626 × 10^-34 J ∙ s)

An electron is in an infinite square well (a box) that is 8.9 nm wide. What is the ground state energy of the electron? (h = 6.626 × 10^-34 J ∙ s, m_el = 9.11 × 10^-31 kg, 1 eV = 1.60 × 10^-19)

A particle confined in a rigid one-dimensional box (an infinite well) of length 17.0 fm has an energy level 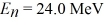and an adjacent energy level E_n+1 = 37.5 MeV. What is the value of the ground state energy? (1 eV = 1.60 × 10^-19 J)