Exam 13: Inference About Comparing Two Populations
Exam 1: What Is Statistics43 Questions
Exam 2: Graphical Descriptive Techniques I93 Questions
Exam 3: Graphical Descriptive Techniques II183 Questions
Exam 4: Numerical Descriptive Techniques274 Questions
Exam 5: Data Collection and Sampling82 Questions
Exam 6: Probability234 Questions
Exam 7: Random Variables and Discrete Probability Distributions274 Questions
Exam 8: Continuous Probability Distributions215 Questions
Exam 9: Sampling Distributions153 Questions
Exam 10: Introduction to Estimation152 Questions
Exam 11: Introduction to Hypothesis Testing182 Questions
Exam 12: Inference About a Population147 Questions
Exam 13: Inference About Comparing Two Populations170 Questions
Exam 14: Analysis of Variance153 Questions
Exam 15: Chi-Squared Tests175 Questions
Exam 16: Simple Linear Regression and Correlation298 Questions
Exam 17: Multiple Regression157 Questions
Select questions type
Two independent samples of sizes 40 and 50 are randomly selected from two populations to test the difference between the population means 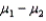 .Assume the population variances are known.The sampling distribution of the sample mean difference
.Assume the population variances are known.The sampling distribution of the sample mean difference 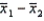 is:
is:
(Multiple Choice)
4.8/5  (38)
(38)
In testing the difference between two population means for which the population variances are unknown and not assumed to be equal, two independent samples are drawn from the populations.Which of the following tests is appropriate?
(Multiple Choice)
4.8/5  (41)
(41)
The expected value of the difference between two sample proportions is the difference between their corresponding population proportions.
(True/False)
4.9/5  (45)
(45)
In testing the difference between the means of two normal populations using two independent samples when the population variances are unequal, the sampling distribution of the resulting statistic is:
(Multiple Choice)
4.9/5  (40)
(40)
In testing the hypothesis 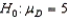 vs.
vs. 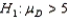 , two random samples from two normal populations produced the following statistics:
, two random samples from two normal populations produced the following statistics: 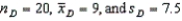 .What conclusion can we draw at the 1% significance level?
.What conclusion can we draw at the 1% significance level?
(Essay)
4.9/5  (34)
(34)
When testing for the difference between two population variances with sample sizes of n1 = 8 and n2 = 10, the degrees of freedom are:
(Multiple Choice)
4.7/5  (27)
(27)
The expected value of the difference between two sample proportions is the ____________________ of/between their corresponding population proportions.
(Short Answer)
4.9/5  (32)
(32)
The pooled proportion estimate is used when the null hypothesis states that the two population proportions differ by ____________________.
(Short Answer)
4.8/5  (42)
(42)
The service manager of a car dealer wants to determine if owners of new cars (two years old or less) tune up their cars more frequently than owners of older cars (more than two years old).From his records he takes a random sample of ten new cars and ten older cars and determines the number of times the cars were tuned up in the last 12 months.The data follow.Do these data allow the service station owner to infer at the 10% significance level that new car owners tune up their cars more frequently than older car owners?
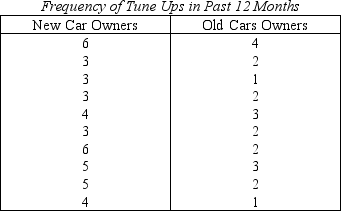
(Essay)
4.8/5  (41)
(41)
In constructing a confidence interval estimate for the difference between the means of two independent normally distributed populations, we:
(Multiple Choice)
4.9/5  (35)
(35)
Random samples from two normal populations produced the following statistics:  ,
, 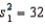 ,
,  , and
, and 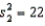 .Is there enough evidence at the 5% significance level to infer that the variance of Population 1 is larger than the variance of Population 2?
.Is there enough evidence at the 5% significance level to infer that the variance of Population 1 is larger than the variance of Population 2?
(Essay)
4.8/5  (32)
(32)
Senatorial Election
A political poll immediately prior to a senatorial election reveals that 145 out of 250 male voters and 105 out of 200 female voters intend to vote for the Democrat candidate.
-{Senatorial Election Narrative} What is the p-value of the test?
(Short Answer)
4.8/5  (27)
(27)
A matched pairs experiment decreases variability (compared to two independent samples).
(True/False)
4.8/5  (34)
(34)
When the population variances are unequal, we estimate each population variance with its sample variance.Hence, the unequal-variances test statistic of 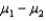 is approximately Student t-distributed with n1 + n2 -2 degrees of freedom.
is approximately Student t-distributed with n1 + n2 -2 degrees of freedom.
(True/False)
4.8/5  (40)
(40)
The sampling distribution of 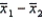 is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n1 and n2 are large.
is normal if the sampled populations are normal, and approximately normal if the populations are nonnormal and the sample sizes n1 and n2 are large.
(True/False)
4.8/5  (33)
(33)
A Marine boot camp instructor recorded the time in which each of 15 recruits completed an obstacle course both before and after basic training.To test whether any improvement occurred, the instructor would use a t-distribution with 15 degrees of freedom.
(True/False)
4.9/5  (28)
(28)
If some natural relationship exists between each pair of observations that provides a logical reason to compare the first observation of sample 1 with the first observation of sample 2, the second observation of sample 1 with the second observation of sample 2, and so on, the samples are referred to as:
(Multiple Choice)
4.9/5  (38)
(38)
The t-test for the difference between the means of two independent populations assumes that the respective:
(Multiple Choice)
4.7/5  (32)
(32)
The pooled proportion estimate is used when the null hypothesis states that the two population proportions differ by some non-zero number.
(True/False)
4.9/5  (39)
(39)
Pooling is made possible by hypothesizing (under the null hypothesis) that p1 __________ p2.
(Short Answer)
4.9/5  (34)
(34)
Showing 81 - 100 of 170
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)