Question 1

Calculate the expected value of X for the given probability distribution. $$\begin{array} { c c c c c } 
x & 0 & 1 & 2 & 3 \
P ( X = x ) & 0.4 & 0.2 & 0.2 & 0.2
\end{array}$$ ​ $$E ( X ) =$$ __________

Accepted Answer

The answer of Calculate the expected value of X for...

Question 2

The following is a sample of the percentage increases in the price of a house from 1980 to 2001 in 8 regions of the U.S.   $75,120,145,155,155,225,225,300$  
Compute the median of the given sample.

Accepted Answer

A)  $m = 155$ 
B)  $m = 120$ 
C)  $m = 175$ 
D)  $m = 225$ 
E)  $m = 145$ 
A)  $m = 155$ 
B)  $m = 120$ 
C)  $m = 175$ 
D)  $m = 225$ 
E)  $m = 145$

Question 3

You are performing 4 independent Bernoulli trials with $p = 0.3$ and $q = 0.7$ . Calculate the probability of no failures. Round your answer to four decimal places if necessary.

Accepted Answer

A) 0.2401 
B)  0.0078 
C)  0.0081 
D)  0.0019 
E)  0.1944 
A) 0.2401 
B)  0.0078 
C)  0.0081 
D)  0.0019 
E)  0.1944

Question 4

The following table shows the distribution of household incomes for a sample of 1,000 households in the U.S. with incomes up to $100,000. 
 
   Use this information to estimate, to the nearest $1,000, the average household income for such households.

Accepted Answer

A)  $\$ 32,000$ 
B)  $\$ 40,000$ 
C)    $\$ 38,000$ 
D)  $\$ 31,000$ 
E)  $\$ 42,000$ 
A)  $\$ 32,000$ 
B)  $\$ 40,000$ 
C)    $\$ 38,000$ 
D)  $\$ 31,000$ 
E)  $\$ 42,000$

Question 5

If we model after-tax household income with a normal distribution, then the figures of a 1995 study imply the information in the following table. Assume that the distribution of incomes in each country is normal, and round all percentages to the nearest whole number. What percentage of U.S. households had an income of $50,000 or more  Express your answer to the nearest 1%. $$\begin{array} { | l | l | l | l | l | l | } 
\hline \text { Country } & \text { U.S. } & \text { Canada } & \text { Switzerland } & \text { Germany } & \text { Sweden } \
\hline \begin{array} { l } 
\text { Mean } \
\text { household } \
\text { income }
\end{array} & \$ 38,000 & \$ 35,000 & \$ 39,000 & \$ 34,000 & \$ 32,000 \
\hline \begin{array} { l } 
\text { Standard } \
\text { deviation }
\end{array} & \$ 21,000 & \$ 17,000 & \$ 16,000 & \$ 14,000 & \$ 11,000 \
\hline
\end{array}$$  
__________% of households

Accepted Answer

The answer of If we model after-tax household income with...

Question 6

Which is smaller: the sample standard deviation or the population standard deviation  ?

Accepted Answer

A) the population standard deviation 
B)  the sample standard deviation 
A) the population standard deviation 
B)  the sample standard deviation

Question 7

X is a binomial variable with $n = 6$ and $p = 0.5$ . Compute $P ( X = 4 )$ . Round your answer to five decimal places.
​ $P ( X = 4 ) =$ __________

Accepted Answer

The answer of X is a binomial variable with \(n...

Question 8

Compute the standard deviation of the data sample.  
 $- 4,3,6,9,14$  
Round your answer to two decimal places if necessary.

Accepted Answer

A) 6.73 
B)  41.92 
C)  22.9 
D)  4.79 
E)  6.02 
A) 6.73 
B)  41.92 
C)  22.9 
D)  4.79 
E)  6.02

Question 9

Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. 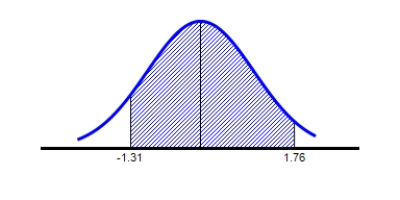  $$P ( - 1.31 < Z < 1.76 )$$      
Round your answer to four decimal places.

Accepted Answer

A)  $P ( - 1.31 < Z < 1.76 ) = 0.8657$ 
B)  $P ( - 1.31 < Z < 1.76 ) = 0.0914$ 
C)    $P ( - 1.31 < Z < 1.76 ) = 0.9608$ 
D)    $P ( - 1.31 < Z < 1.76 ) = 0.0951$ 
E)    $P ( - 1.31 < Z < 1.76 ) = 0.0559$ 
A)  $P ( - 1.31 < Z < 1.76 ) = 0.8657$ 
B)  $P ( - 1.31 < Z < 1.76 ) = 0.0914$ 
C)    $P ( - 1.31 < Z < 1.76 ) = 0.9608$ 
D)    $P ( - 1.31 < Z < 1.76 ) = 0.0951$ 
E)    $P ( - 1.31 < Z < 1.76 ) = 0.0559$

Question 10

Your scores for the 20 surprise math quizzes last semester were (out of 10) $$\begin{array} { l l l l l l l l l l l } 
5.5&9.5&10.0&3.5&8.0&9.5&7.5&6.5&6.0&8.0\8.0&8.5&7.5&6.0&8.0&10.0&10.0&8.5&7.&8.0
\end{array}$$ Use these raw data to construct a frequency table: $$\begin{array} { l | l | l | l | l | } 
\hline \text { Score } & 2.1 - 4.0 & 4.1 - 6.0 & 6.1 - 8.0 & 8.1 - 10.0 \
\hline \text { Frequency } & & & & \
\hline
\end{array}$$ ​
Find the probability distribution using the (rounded) midpoint values as the values of X. $$\begin{array} { c | l | l | l | l | } 
\hline x & 3.0 & 5.0 & 7.0 & 9.0 \
\hline P ( X = x ) & & & & \
\hline
\end{array}$$

Accepted Answer

1; 3; 9; 7

Question 11

The following table shows the approximate number of males of Hispanic origin employed in the U.S. in 2005, broken down by age group. In what age interval does the empirical rule predict that 68 percent of all male Hispanic workers will fall  Please round answers to the nearest year. $$\begin{array} { | c | c | c | c | } 
\hline \text { Age } & 15 - 24.9 & 25 - 54.9 & 55 - 64.9 \
\hline \begin{array} { c } 
\text { Employment } \
\text { (thousands) }
\end{array} & 16,000 & 13,000 & 1,600 \
\hline
\end{array}$$

Accepted Answer

A) 31 - 42 
B)  19 - 31 
C)  19 - 42 
D)  12 - 31 
E)  12 - 42 
A) 31 - 42 
B)  19 - 31 
C)  19 - 42 
D)  12 - 31 
E)  12 - 42

Question 12

You are performing 5 independent Bernoulli trials with $p = 0.2$ and $q = 0.8$ . Calculate the probability of 2 successes. Round your answer to five decimal places if necessary.

Accepted Answer

A)  0.4 
B)   0.0512 
C)   0.04 
D)   0.512 
E)   0.2048 
A)  0.4 
B)   0.0512 
C)   0.04 
D)   0.512 
E)   0.2048

Question 13

The probability that a randomly selected pound of beef is purchased by McDonald's is 0.06. Ten pounds of beef are chosen at random.
What is the probability that exactly two of them are purchased by McDonald's  Round your answer to four decimal places.
The probability is __________.
Use technology to generate the probability distribution for the associated binomial random variable. Round your answers to four decimal places. $\begin{array} { | c | c | c | c | c | c | } 
\hline x & 0 & 1 & 2 & 3 & 4 \
\hline P ( X = x ) & & & & & \
\hline 5 & 6 & 7 & 8 & 9 & 10 \
\hline & & & & & \
\hline
\end{array}$ ?
If 10 pounds of beef produced in the U.S. are selected at random, the number of pounds most likely to have been purchased by McDonald's is __________.

Accepted Answer

0.0988; 0.5386; 0.34

Question 14

Your manufacturing plant produces air bags, and it is known that 50% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places.

Accepted Answer

The answer of Your manufacturing plant produces air bags, and...

Question 15

X is a binomial variable with $n = 4$ and $p = \frac { 1 } { 2 }$ . Compute the probability correct to four decimal places $P ( 0 \leq X \leq 2 )$ .
​ $P ( 0 \leq X \leq 2 ) \approx$ __________

Accepted Answer

The answer of X is a binomial variable with \(n...

Question 16

X is a binomial variable with and $p = \frac { 1 } { 5 }$ . Compute the probability $P ( 0 < X < 2 )$ . Round your answer to four decimal places .

Accepted Answer

A)  $P ( 0 \leq X \leq 2 ) = 0.0563$ 
B)  $P ( 0 \leq X \leq 2 ) = 0.5632$ 
C)  $P ( 0 \leq X \leq 2 ) = 0.0272$ 
D)  $P ( 0 \leq X \leq 2 ) = 0.41$ 
E)  $P ( 0 \leq X \leq 2 ) = 0.9728$ 
A)  $P ( 0 \leq X \leq 2 ) = 0.0563$ 
B)  $P ( 0 \leq X \leq 2 ) = 0.5632$ 
C)  $P ( 0 \leq X \leq 2 ) = 0.0272$ 
D)  $P ( 0 \leq X \leq 2 ) = 0.41$ 
E)  $P ( 0 \leq X \leq 2 ) = 0.9728$

Question 17

Given the data.
​ $1,0 , - 2,1,5$ ​
Compute the mean.
​ $\bar { x } =$ __________
​
Compute the median.
​ $m =$ __________
​
Compute the mode.
​
__________

Accepted Answer

The answer of Given the data.
​ $1,0 , - 2,1,5$...

Question 18

In a large on-the-job training program, half of the participants are female and half are male. In a random sample of 4 participants, what is the probability that an investigator will draw at least 1 male  Please, round your answer to four decimal places.

Accepted Answer

A) 0.9375 
B)  0.0312 
C)  0.25 
D)  0.9899 
E)  0.875 
A) 0.9375 
B)  0.0312 
C)  0.25 
D)  0.9899 
E)  0.875

Question 19

The following list shows the percentage of aging population (residents of age 65 and older) in each of the 50 states in 1990 and 2000.  
2000
  $$\begin{array} { l } 
6,9,10,10,10,11,11,11,11,11 , \
11,11,12,12,12,12,12,12,12,12 , \
12,12,12,13,13,13,13,13,13,13 , \
13,13,13,13,13,13,13,14,14,14 , \
14,14,14,14,15,15,15,15,16,18
\end{array}$$  
1990
  $$\begin{array} { l } 
4,9,10,10,10,10,10,11,11,11 , \
11,11,11,11,11,12,12,12,12,12 , \
12,13,13,13,13,13,13,13,13,13 , \
13,13,13,13,13,14,14,14,14,14 , \
14,14,14,15,15,15,15,15,15,18
\end{array}$$  
What was the actual percentage of states whose aging population in 1990 was within two standard deviations of the mean  Round your answer to one decimal place if necessary.

Accepted Answer

A) 96% 
B)  95% 
C)  97% 
D)  75% 
E)  86% 
A) 96% 
B)  95% 
C)  97% 
D)  75% 
E)  86%

Question 20

Your manufacturing plant produces air bags, and it is known that 2% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places if necessary. ​

Accepted Answer

A) ​0.2614 
B)  ​0.0353 
C)  ​0.003 
D)  ​0.7386 
E)  ​0.997 
A) ​0.2614 
B)  ​0.0353 
C)  ​0.003 
D)  ​0.7386 
E)  ​0.997

Calculate the expected value of X for the given probability distribution. x 0 1 2 3 P(X=x) 0.4 0.2 0.2 0.2 $E ( X ) =$ __________

The following is a sample of the percentage increases in the price of a house from 1980 to 2001 in 8 regions of the U.S. $75,120,145,155,155,225,225,300$ Compute the median of the given sample.

You are performing 4 independent Bernoulli trials with $p = 0.3$ and $q = 0.7$ . Calculate the probability of no failures. Round your answer to four decimal places if necessary.

The following table shows the distribution of household incomes for a sample of 1,000 households in the U.S. with incomes up to $100,000. Use this information to estimate, to the nearest $1,000, the average household income for such households.

Which is smaller: the sample standard deviation or the population standard deviation ?

X is a binomial variable with $n = 6$ and $p = 0.5$ . Compute $P ( X = 4 )$ . Round your answer to five decimal places. $P ( X = 4 ) =$ __________

Compute the standard deviation of the data sample. $- 4,3,6,9,14$ Round your answer to two decimal places if necessary.

Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. $P ( - 1.31 < Z < 1.76 )$ Round your answer to four decimal places.

You are performing 5 independent Bernoulli trials with $p = 0.2$ and $q = 0.8$ . Calculate the probability of 2 successes. Round your answer to five decimal places if necessary.

Your manufacturing plant produces air bags, and it is known that 50% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places.

X is a binomial variable with $n = 4$ and $p = \frac { 1 } { 2 }$ . Compute the probability correct to four decimal places $P ( 0 \leq X \leq 2 )$ . $P ( 0 \leq X \leq 2 ) \approx$ __________

X is a binomial variable with and $p = \frac { 1 } { 5 }$ . Compute the probability $P ( 0 < X < 2 )$ . Round your answer to four decimal places .

Given the data. $1,0 , - 2,1,5$ Compute the mean. $\bar { x } =$ Compute the median. $m =$ Compute the mode. __

In a large on-the-job training program, half of the participants are female and half are male. In a random sample of 4 participants, what is the probability that an investigator will draw at least 1 male Please, round your answer to four decimal places.

Your manufacturing plant produces air bags, and it is known that 2% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places if necessary.

Functions and Applications

Nonlinear Functions and Models

The Mathematics of Finance

Systems of Linear Equations and Matrices

Matrix Algebra and Applications

Linear Programming

Sets and Counting

Probability

Introduction to the Derivative

Techniques of Differentiation

Applications of the Derivative

The Integral

Further Integration Techniques and Applications of the Integral

Functions of Several Variables

Trigonometric Models

Filters

Exam 9: Random Variables and Statistics

Calculate the expected value of X for the given probability distribution. x 0 1 2 3 P(X=x) 0.4 0.2 0.2 0.2 ​ E(X)=E ( X ) =E(X)= __________

The following is a sample of the percentage increases in the price of a house from 1980 to 2001 in 8 regions of the U.S. 75,120,145,155,155,225,225,30075,120,145,155,155,225,225,30075,120,145,155,155,225,225,300 Compute the median of the given sample.

You are performing 4 independent Bernoulli trials with p=0.3p = 0.3p=0.3 and q=0.7q = 0.7q=0.7 . Calculate the probability of no failures. Round your answer to four decimal places if necessary.

The following table shows the distribution of household incomes for a sample of 1,000 households in the U.S. with incomes up to $100,000. Use this information to estimate, to the nearest $1,000, the average household income for such households.

Which is smaller: the sample standard deviation or the population standard deviation ?

X is a binomial variable with n=6n = 6n=6 and p=0.5p = 0.5p=0.5 . Compute P(X=4)P ( X = 4 )P(X=4) . Round your answer to five decimal places. ​ P(X=4)=P ( X = 4 ) =P(X=4)= __________

Compute the standard deviation of the data sample. −4,3,6,9,14- 4,3,6,9,14−4,3,6,9,14 Round your answer to two decimal places if necessary.

Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. P(−1.31<Z<1.76)P ( - 1.31 < Z < 1.76 )P(−1.31<Z<1.76) Round your answer to four decimal places.

You are performing 5 independent Bernoulli trials with p=0.2p = 0.2p=0.2 and q=0.8q = 0.8q=0.8 . Calculate the probability of 2 successes. Round your answer to five decimal places if necessary.

Your manufacturing plant produces air bags, and it is known that 50% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places.

X is a binomial variable with n=4n = 4n=4 and p=12p = \frac { 1 } { 2 }p=21​ . Compute the probability correct to four decimal places P(0≤X≤2)P ( 0 \leq X \leq 2 )P(0≤X≤2) . ​ P(0≤X≤2)≈P ( 0 \leq X \leq 2 ) \approxP(0≤X≤2)≈ __________

X is a binomial variable with and p=15p = \frac { 1 } { 5 }p=51​ . Compute the probability P(0<X<2)P ( 0 < X < 2 )P(0<X<2) . Round your answer to four decimal places .

Given the data. ​ 1,0,−2,1,51,0 , - 2,1,51,0,−2,1,5 ​ Compute the mean. ​ xˉ=\bar { x } =xˉ= __________ ​ Compute the median. ​ m=m =m= __________ ​ Compute the mode. ​ __________

In a large on-the-job training program, half of the participants are female and half are male. In a random sample of 4 participants, what is the probability that an investigator will draw at least 1 male Please, round your answer to four decimal places.

Your manufacturing plant produces air bags, and it is known that 2% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places if necessary. ​

Functions and Applications

Nonlinear Functions and Models

The Mathematics of Finance

Systems of Linear Equations and Matrices

Matrix Algebra and Applications

Linear Programming

Sets and Counting

Probability

Introduction to the Derivative

Techniques of Differentiation

Applications of the Derivative

The Integral

Further Integration Techniques and Applications of the Integral

Functions of Several Variables

Trigonometric Models

Filters

Calculate the expected value of X for the given probability distribution. x 0 1 2 3 P(X=x) 0.4 0.2 0.2 0.2 $E ( X ) =$ __________

The following is a sample of the percentage increases in the price of a house from 1980 to 2001 in 8 regions of the U.S. $75,120,145,155,155,225,225,300$ Compute the median of the given sample.

You are performing 4 independent Bernoulli trials with $p = 0.3$ and $q = 0.7$ . Calculate the probability of no failures. Round your answer to four decimal places if necessary.

X is a binomial variable with $n = 6$ and $p = 0.5$ . Compute $P ( X = 4 )$ . Round your answer to five decimal places. $P ( X = 4 ) =$ __________

Compute the standard deviation of the data sample. $- 4,3,6,9,14$ Round your answer to two decimal places if necessary.

Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve. $P ( - 1.31 < Z < 1.76 )$ Round your answer to four decimal places.

You are performing 5 independent Bernoulli trials with $p = 0.2$ and $q = 0.8$ . Calculate the probability of 2 successes. Round your answer to five decimal places if necessary.

X is a binomial variable with $n = 4$ and $p = \frac { 1 } { 2 }$ . Compute the probability correct to four decimal places $P ( 0 \leq X \leq 2 )$ . $P ( 0 \leq X \leq 2 ) \approx$ __________

X is a binomial variable with and $p = \frac { 1 } { 5 }$ . Compute the probability $P ( 0 < X < 2 )$ . Round your answer to four decimal places .

Given the data. $1,0 , - 2,1,5$ Compute the mean. $\bar { x } =$ Compute the median. $m =$ Compute the mode. __

Your manufacturing plant produces air bags, and it is known that 2% of them are defective. Fifteen air bags are tested. Find the probability that at least two of them are defective. Round your answer to four decimal places if necessary.