Exam 9: Random Variables and Statistics
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
Assume that on a standardized test of 100 questions, a person has a probability of 84% of answering any particular question correctly. Find the probability of answering between 75 and 85 questions, inclusive, correctly. (Assume independence, and round your answer to four decimal places.)
(Short Answer)
4.8/5  (37)
(37)
The mathematics final exam scores for the students in your study group are 89%, 83%, 95%, 67%, 92%, and 80%.
List the values of X for all the outcomes.
(Multiple Choice)
4.7/5  (33)
(33)
X is a binomial variable with and . Compute . Round your answer to five decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
According to a July, 1999, article in the New York Times, 13.5% of Internet stocks that entered the market in 1999 ended up trading below their initial offering prices. If you were an investor who purchased 11 Internet stocks at their initial offering prices, what was the probability that at least 10 of them would end up trading at or above their initial offering price (Round your answer to four decimal places.) ?
(Multiple Choice)
4.8/5  (32)
(32)
You are performing five independent Bernoulli trials with and . Calculate the probability of no failures. Round your answer to four decimal places.
(Short Answer)
4.7/5  (36)
(36)
According to a study, the probability that a randomly selected teenager watched a rented video at least once during a week was 0.78. What is the probability that at least 8 teenagers in a group of 10 watched a rented movie at least once last week Express your answer to the nearest hundredth. ?
(Multiple Choice)
4.9/5  (42)
(42)
A random variable has the probability distribution table as shown. Calculate . -3 -2 -1 0 1 ( =x) 0.5 0.2 0.1 __________
(Short Answer)
4.8/5  (33)
(33)
It is known that 69% of all the ZeroCal hamburger patties produced by your factory actually contain more than 1,000 calories. Compute the probability distribution for Bernoulli trials. What is the most likely value for the number of burgers in a sample of 50 that contain more than 1,000 calories
(Multiple Choice)
4.8/5  (32)
(32)
Compute the (sample) variance and the standard deviation for the data.
Please round your answers to two decimal places, if necessary.
__________
__________
(Short Answer)
4.7/5  (42)
(42)
Give a sample of 9 scores with mean 1 and with median ≠ mean. Arrange the scores in ascending order.
(Essay)
4.8/5  (35)
(35)
Give a sample of 8 scores with mean 1 and with median ≠ mean. Arrange the scores in ascending order.
(Multiple Choice)
4.9/5  (44)
(44)
If we model after-tax household income with a normal distribution, then the figures of a 1995 study imply the information in the following table. Assume that the distribution of incomes in each country is normal, and round all percentages to the nearest whole number. What percentage of German households are either very wealthy (income at least $100,000) or very poor (income at most $12,000) Express your answer to the nearest 1%. Country U.S. Canada Switzerland Germany Sweden Mean household income \ 38,000 \ 35,000 \ 39,000 \ 34,000 \ 32,000 Standard deviation \ 21,000 \ 17,000 \ 16,000 \ 14,000 \ 11,000
__________% of households
(Short Answer)
4.9/5  (35)
(35)
Find the value of the probability of the standard normal variable Z corresponding to the shaded area under the standard normal curve.
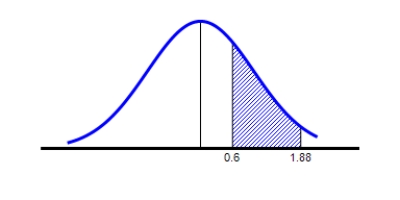
Round your answer to four decimal places.
__________
Round your answer to four decimal places.
__________
(Short Answer)
4.9/5  (35)
(35)
The table shows crashworthiness ratings for several categories of motor vehicles. Take X as the crash-test rating of a small car, Y as the crash-test rating for a small SUV, and so on, as shown in the table. Overall Frontal Crash Test Rating Number Tested (Good) (Acceptable) (Marginal) (Poor) Small Cars X 20 1 13 3 3 Small SUVs Y 10 1 4 4 1 Medium SUVs Z 15 3 5 3 4 Passenger Vans U 13 3 0 3 7 Midsize Cars V 15 3 5 0 7 Large Cars W 19 9 5 3 2 Compute .

(Multiple Choice)
4.9/5  (25)
(25)
11 darts are thrown at a dartboard. The probability of hitting a bull's-eye is 0.1. Let X be the number of bull's-eyes hit. Calculate the expected value of the given random variable X.
__________
(Short Answer)
4.9/5  (29)
(29)
Find the expected value of a random variable X having the following probability distribution: x 2 4 6 8 P(X=x) __________
(Short Answer)
4.9/5  (37)
(37)
A random variable has the probability distribution table as shown. Calculate . 1 3 5 7 9 ( = ) 0.2 0.1 0.3 0.2
(Multiple Choice)
4.9/5  (35)
(35)
Assume that on a standardized test of 100 questions, a person has a probability of 86% of answering any particular question correctly. Find the probability of answering between 75 and 85 questions, inclusive, correctly. (Assume independence, and round your answer to four decimal places.)
(Multiple Choice)
4.9/5  (27)
(27)
Showing 101 - 120 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)