Exam 23: Time-Series Analysis and Forecasting

In an exponentially smoothed time series, the smoothing constant w is chosen on the basis of how much smoothing is required. In general, a small value of w such as 0.1 results in a great deal of smoothing, while a large value of w, such as 0.9, results in very little smoothing.

If we wanted to measure the seasonal variations on stock market performance by month, we would need:

The trend equation for annual sales data (in millions of dollars) is 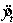$=65+2.5 t$ , where t = 1 for 2000. The monthly seasonal index for December is 0.97. The forecast sales for December of 2009 is:

The level of construction employment in Sydney is lowest during the winter. A model designed to forecast construction employment in Sydney should use:

In general, it is easy to identify the trend component of a time series by using:

Smoothing time-series data by the moving average method or exponential smoothing method is an attempt to remove the effect of the random variation component.

In determining weekly seasonal indexes for petrol consumption, the sum of the 52 means for petrol consumption as a percentage of the moving average is 5050. To get the seasonal indexes, each weekly mean is to be multiplied by:

Quarterly sales revenue (in $million) for a particular company has been modelled using linear regression with indicator variables: Y = 132 + 2Q₁ + 3Q₂ - 5Q₄ + 2t Where t is time in quarters, with origin March 2006 and Q₁, Q₂ and Q₄ are the indicator variables for March, June and December quarters, respectively. Describe the trend and seasonal effects.

The stock market has a 5-day working week. If we wanted to measure the impact of the day of the week on stock market performance, we would need:

In measuring the cyclical effect of a time series, cycles need to be isolated. The measure we use to identify cyclical variation is the:

Annual production (in millions) of computer chips in a large electronics company was recorded, as shown below. Year t Production 1990 1 26 1991 2 23 1992 3 21 1993 4 25 1994 5 32 1995 6 38 1996 7 43 1997 8 36 1998 9 29 1999 10 25 a. Calculate the percentage of trend for each time period. b. Plot the percentage of trend. c. Describe the cyclical effect (if there is one).

In an exponentially smoothed time series, the smoothing constant w is chosen on the basis of how much smoothing is required. In general:

The number of pairs of sunglasses sold each quarter in a beachside drugstore were recorded for the years 2007-2010. These data are shown in the following table. Year Quarter 2007 2008 2009 2010 1 82 84 85 90 2 72 71 70 74 3 65 66 67 71 4 53 54 56 58 a. Develop a regression model, using indicator variables to represent quarters. b. Forecast the quarterly earnings for the years 2011 and 2012.

a. Plot the following time series. Would the linear or quadratic model fit better? Time period Time period 1 5 5 50 2 8 6 85 3 14 7 135 4 25 8 190 b. Use the regression technique to calculate the linear trend line and the quadratic trend line. c. Which line fits better?

Which of the following methods may be used to smooth a time series sufficiently to remove the random variation and to discover the existence of the other time-series components?

One application of seasonal indexes is to remove the seasonal variation in a time series. The process is called deseasonalising, and the result is called a seasonally adjusted time series.

Use exponential smoothing, with w = 0.23 to forecast the next value of the time series below. t 1 20 2 16 3 24 4 25 5 22 6 21

Which of the following smoothing constants causes the most rapid reaction to a change in the current time-series value?

The easiest way of measuring the long-term trend is through regression analysis, where time is the dependent variable.

A company selling swimming goggles wants to analyze its Australian sales figures. Time series forecasting with regression was used to generate Excel output to estimate trend and seasonal effects of the time series of Swimming goggle sales (in thousands of dollars) where the origin is the March Quarter 2000 and Q₁ denotes sales in the March quarter, Q₃ denotes sales in the September quarter and Q₄ denotes sales in the December quarter. SUMMARY OUTPUT Regression Statistios Multiple R 0.9460 R Square 0.8950 Adjusted R Square 0.8864 Standard Error 3.7394 obseruations 54 ANOVA Signficance df SS MS F F Regression 4 5837.596003 1459.4 104.3701 2.41949-23 Residual 49 685.1632564 13.9829 Total 53 6522.759259 Standard Upper Coeffcients Error t Stat P-value Lower 95\% 95\% Intercept 3.0588 1.3331 2.2944 0.0261 0.3797 5.7378 0.2518 0.0327 7.7052 0.0000 0.1861 0.3175 1 12.4604 1.3897 8.9664 0.0000 9.6677 15.2530 3 1.1458 1.4721 0.7784 0.4401 -1.8124 4.1041 23.9121 1.4403 16.6025 0.0000 21.0177 26.8064 (a) Write out the regression equations for each of the four quarters. (b) Sketch the four equations from part (a) on the same set of axes. (c) Interpret the coefficients on all the indicator variables. (c) All the indicator variables have positive coefficients. Is this surprising? Explain.