Exam 23: Time-Series Analysis and Forecasting
Exam 1: What Is Statistics14 Questions
Exam 2: Types of Data, Data Collection and Sampling16 Questions
Exam 3: Graphical Descriptive Methods Nominal Data19 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures147 Questions
Exam 6: Probability106 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions117 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions65 Questions
Exam 11: Estimation: Describing a Single Population127 Questions
Exam 12: Estimation: Comparing Two Populations22 Questions
Exam 13: Hypothesis Testing: Describing a Single Population129 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations78 Questions
Exam 15: Inference About Population Variances49 Questions
Exam 16: Analysis of Variance115 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests110 Questions
Exam 18: Simple Linear Regression and Correlation213 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building92 Questions
Exam 21: Nonparametric Techniques126 Questions
Exam 22: Statistical Inference: Conclusion103 Questions
Exam 23: Time-Series Analysis and Forecasting145 Questions
Exam 24: Index Numbers25 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
The term 'seasonal variation' may refer to the four traditional seasons, or to systematic patterns that occur during a quarter, a week, or even one day, but within 12 months.
(True/False)
4.7/5  (32)
(32)
The high level of airline ticket sales that travel agencies experience during summer is an example of which component of a time series?
(Multiple Choice)
4.8/5  (40)
(40)
Regression analysis with t = 1 to 80 was used to develop the following forecast equation:
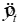 = 135 + 4.8t - 1.3Q1 - 1.7Q2 + 1.5Q3
where:
Qi = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four values.
= 135 + 4.8t - 1.3Q1 - 1.7Q2 + 1.5Q3
where:
Qi = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four values.
(Essay)
4.9/5  (38)
(38)
The model that assumes the time-series value at time t is the sum of the four time-series components is referred to as the:
(Multiple Choice)
4.8/5  (38)
(38)
A time series for the years 1990-1995 is shown below. Year 1990 125 1991 115 1992 120 1993 126 1994 140 1995 122 a. Develop forecasts for the years 1996-1998, with the following smoothing constant values:
w = 0.2, w = 0.5 and w = 0.6.
b. Compare each of the three sets of forecasts above with the actual values for 1996-1998 given in the following table, and compute the MAD for each model. Which model is best? Year 1996 130 1997 125 1998 135
(Essay)
4.9/5  (32)
(32)
The following trend line and seasonal indexes were computed from four weeks of daily observations. 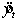 . Day S Sunday 1.403 Monday 0.517 Tuesday 0.515 Wednesday 0.621 Thursday 0.675 Friday 1.145 Saturday 2.124 Forecast the seven values for the next week.
. Day S Sunday 1.403 Monday 0.517 Tuesday 0.515 Wednesday 0.621 Thursday 0.675 Friday 1.145 Saturday 2.124 Forecast the seven values for the next week.
(Essay)
4.8/5  (31)
(31)
The most commonly used measures of forecast accuracy are the:
(Multiple Choice)
4.8/5  (35)
(35)
The result of a quadratic model fit to time-series data was 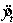 , where t = 1 for 1994. The forecast value for 2001 is 129.25.
, where t = 1 for 1994. The forecast value for 2001 is 129.25.
(True/False)
4.8/5  (37)
(37)
The actual and forecast values of a time series are shown below. Actual values Forecast values 135 140 162 165 155 150 182 191 174 168 194 190 233 220 280 240 a. Calculate the mean absolute deviation (MAD).
b. Calculate the sum of squares for forecast error (SSE).
(Essay)
4.8/5  (29)
(29)
To calculate the random component of a time series, ignoring the cyclical component, it would be the difference between an actual observation and the predicted value using a regression model with indicator variables for the seasonal component and time as the trend component.
(True/False)
4.9/5  (34)
(34)
Regression analysis with t = 1 to 40 was used to develop the following equation: 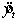 ,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four quarters.
,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four quarters.
(Essay)
4.9/5  (38)
(38)
One of the simplest ways to reduce random variation is to smooth the time series via moving averages and exponential smoothing.
(True/False)
4.8/5  (35)
(35)
The smoothing component is one of the four components of a time series.
(True/False)
4.7/5  (38)
(38)
A time series regression model using quarterly time periods will only use three quarters as the indicator variables.
(True/False)
4.9/5  (33)
(33)
The following are the values of a time series for the first four time periods: t 1 2 3 4 23 25 28 24 Using exponential smoothing, with w = 0.25, the forecast value for time period 5 is:
(Multiple Choice)
4.9/5  (42)
(42)
The regression trend line for annual energy consumption for 1985-2005 is given by ŷt = 70 + 0.53t, where t = 1 for 1985. If the annual energy consumption for 2000 was 82.5, then the percentage of trend for 2000 was:
(Multiple Choice)
4.8/5  (39)
(39)
Which of the following methods is appropriate for forecasting a time series when the trend, cyclical and seasonal components of the series are not significant?
(Multiple Choice)
4.9/5  (41)
(41)
Quarterly enrolments in a business statistics class for three years are shown below. Year Quarter Enrolment 1996 1 26 2 29 3 33 4 18 1997 1 27 2 25 3 36 4 21 1998 1 32 2 36 3 39 4 30 Compute the four-quarter centred moving averages.
(Essay)
4.7/5  (37)
(37)
Which of the following are examples of seasons when measuring the seasonal component of a time series?
(Multiple Choice)
4.8/5  (34)
(34)
Showing 121 - 140 of 145
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)