Exam 9: Project Scheduling: Pertcpm

Activities G, P, and R are the immediate predecessors for activity W. If the earliest finish times for the three are 12, 15, and 10, then the earliest start time for W

Given the following network with activities and times estimated in days, 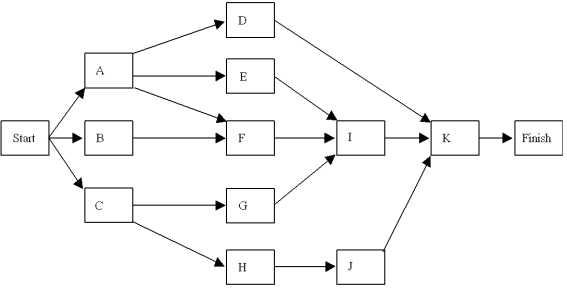Most Activity Optimistic Probable Pessimistic A 2 5 6 B 1 3 7 C 6 7 10 D 5 12 14 E 3 4 5 F 8 9 12 G 4 6 8 H 3 6 8 I 5 7 12 J 12 13 14 K 1 3 4 a.What are the critical path activities? b.What is the expected time to complete the project? c.What is the probability the project will take more than 28 days to complete?

Explain how and why all predecessor activities must be considered when finding the earliest start time.

The critical path for this network is A - E - F and the project completion time is 22 weeks. 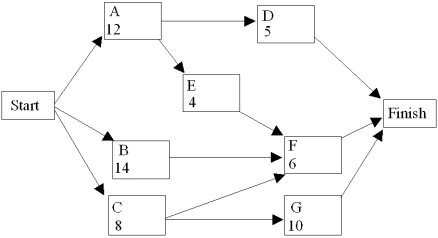Activity Normal Time Crash Time Normal Cost Crash Cost A 12 8 8,000 12,000 B 14 10 5,000 7,500 C 8 8 10,000 10,000 D 5 3 6,000 8,000 E 4 3 5,000 7,000 F 6 5 9,000 12,000 G 10 8 5,000 8,000 If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.

When activity times are uncertain,

For an activity with more than one immediate predecessor activity, which of the following is used to compute its earliest finish (EF) time?

When activity times are uncertain, total project time is normally distributed with mean equal to the sum of the means of all of the critical activities.

Activities with zero slack

A critical activity can be part of a noncritical path.

Critical activities are those that can be delayed without delaying the entire project.

The earliest start time for an activity is equal to the smallest of the earliest finish times for all its immediate predecessors.

Activities following a node

A path through a project network must reach every node.

The earliest start time rule

Slack equals

From this schedule of activities, draw the PERT/CPM network. Activity Immediate Predecessor A \@cdots B A C B D B E A F C, D G E, F

A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. 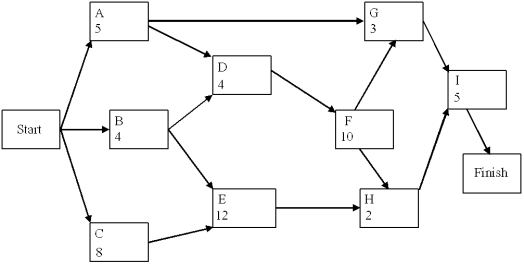Activity Immediate Predecessors Activity Time (weeks) ES LS EF LF Sack Critical Path? Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?

The critical path

Once the earliest and latest times are calculated, how is the critical path determined?

In deciding which activities to crash, one must