Exam 13: Experimental Design and Analysis of Variance
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures118 Questions
Exam 4: Introduction to Probability94 Questions
Exam 5: Discrete Probability Distributions84 Questions
Exam 6: Continuous Probability Distributions121 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Interval Estimation90 Questions
Exam 9: Hypothesis Tests95 Questions
Exam 10: Inference About Means and Proportions With Two Populations63 Questions
Exam 11: Inferences About Population Variances66 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance76 Questions
Exam 14: Simple Linear Regression132 Questions
Exam 15: Multiple Regression103 Questions
Exam 16: Regression Analysis: Model Building41 Questions
Exam 17: Time Series Analysis and Forecasting51 Questions
Exam 18: Nonparametric Methods58 Questions
Exam 19: Decision Analysis48 Questions
Exam 20: Index Numbers39 Questions
Exam 21: Statistical Methods for Quality Control60 Questions
Exam 22: Sample Survey48 Questions
Select questions type
The number of times each experimental condition is observed in a factorial design is known as
(Multiple Choice)
4.8/5  (26)
(26)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to within-treatments is
(Multiple Choice)
4.8/5  (34)
(34)
An experimental design where the experimental units are randomly assigned to the treatments is known as _____ design.
(Multiple Choice)
4.9/5  (29)
(29)
In an analysis of variance problem if SST = 120 and SSTR = 90, then SSE is
(Multiple Choice)
4.8/5  (33)
(33)
Consider the following ANOVA table. 
The mean square due to treatments equals
The mean square due to treatments equals
(Multiple Choice)
4.8/5  (37)
(37)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The mean square due to error (MSE) is
(Multiple Choice)
4.8/5  (43)
(43)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 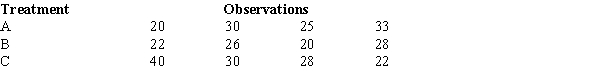
The null hypothesis for this ANOVA problem is
The null hypothesis for this ANOVA problem is
(Multiple Choice)
4.7/5  (34)
(34)
Part of an ANOVA table is shown below.  At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is that
At a 5% level of significance, if we want to determine whether or not the means of the populations are equal, the conclusion of the test is that
(Multiple Choice)
4.8/5  (34)
(34)
Consider the following ANOVA table. 
The sum of squares due to error equals
The sum of squares due to error equals
(Multiple Choice)
4.8/5  (34)
(34)
If we are testing for the equality of three population means, we should use the
(Multiple Choice)
4.7/5  (36)
(36)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). The following information is provided.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
If we want to determine whether or not the means of the five populations are equal, the p-value is
(Multiple Choice)
4.9/5  (31)
(31)
Consider the following ANOVA table. 
The null hypothesis is to be tested at the 1% level of significance. The p-value is
The null hypothesis is to be tested at the 1% level of significance. The p-value is
(Multiple Choice)
5.0/5  (37)
(37)
Part of an ANOVA table is shown below.  The number of degrees of freedom corresponding to within-treatments is
The number of degrees of freedom corresponding to within-treatments is
(Multiple Choice)
4.9/5  (36)
(36)
The test scores for selected samples of sociology students who took the course from three different instructors are shown below. 
At α = .05, test to see if there is a significant difference among the averages of the three groups. Use both the critical value and p-value approaches.
At α = .05, test to see if there is a significant difference among the averages of the three groups. Use both the critical value and p-value approaches.
(Essay)
4.7/5  (28)
(28)
Random samples of employees from three different departments of MNM Corporation showed the following yearly incomes (in $1000). 
At α = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments. Use both the critical and p-value approaches.
At α = .05, test to determine if there is a significant difference among the average incomes of the employees from the three departments. Use both the critical and p-value approaches.
(Essay)
4.9/5  (30)
(30)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). The following information is provided.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The test statistic is
(Multiple Choice)
5.0/5  (36)
(36)
The critical F value with 6 numerator and 40 denominator degrees of freedom at α = .05 is
(Multiple Choice)
4.9/5  (40)
(40)
Consider the following information. 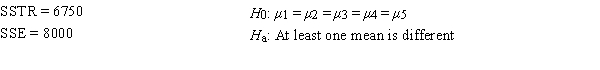
If n = 5, the mean square due to error (MSE) equals
If n = 5, the mean square due to error (MSE) equals
(Multiple Choice)
4.9/5  (32)
(32)
The heating bills for a selected sample of houses in a city using various forms of heating are given below (values are in dollars). 
At α = .05, test to see if there is a significant difference among the average bills of all the homes (in a city) using three forms of heating. Use both the critical and p-value approaches.
At α = .05, test to see if there is a significant difference among the average bills of all the homes (in a city) using three forms of heating. Use both the critical and p-value approaches.
(Essay)
4.8/5  (37)
(37)
MNM, Inc. has three stores located in three different areas. Random samples of the daily sales of the three stores (in $1000) are shown below. 
At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores. Use both the critical and p-value approaches.
At the 1% level of significance, test to see if there is a significant difference in the average sales of the three stores. Use both the critical and p-value approaches.
(Essay)
4.9/5  (36)
(36)
Showing 21 - 40 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)