Exam 13: Experimental Design and Analysis of Variance
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures118 Questions
Exam 4: Introduction to Probability94 Questions
Exam 5: Discrete Probability Distributions84 Questions
Exam 6: Continuous Probability Distributions121 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Interval Estimation90 Questions
Exam 9: Hypothesis Tests95 Questions
Exam 10: Inference About Means and Proportions With Two Populations63 Questions
Exam 11: Inferences About Population Variances66 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance76 Questions
Exam 14: Simple Linear Regression132 Questions
Exam 15: Multiple Regression103 Questions
Exam 16: Regression Analysis: Model Building41 Questions
Exam 17: Time Series Analysis and Forecasting51 Questions
Exam 18: Nonparametric Methods58 Questions
Exam 19: Decision Analysis48 Questions
Exam 20: Index Numbers39 Questions
Exam 21: Statistical Methods for Quality Control60 Questions
Exam 22: Sample Survey48 Questions
Select questions type
Part of an ANOVA table is shown below.  The number of degrees of freedom corresponding to between-treatments is
The number of degrees of freedom corresponding to between-treatments is
(Multiple Choice)
4.9/5  (29)
(29)
When an analysis of variance is performed on samples drawn from k populations, the mean square due to treatments (MSTR) is
(Multiple Choice)
4.8/5  (38)
(38)
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to between-treatments is
(Multiple Choice)
4.9/5  (37)
(37)
Three universities in your state decided to administer the same comprehensive examination to the recipients of MBA degrees from the three institutions. From each institution, MBA recipients were randomly selected and were given the test. The following table shows the scores of the students tested by each university. 
At α = .01, test to see if there is any significant difference in the average scores of all the students who took the exam from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.
At α = .01, test to see if there is any significant difference in the average scores of all the students who took the exam from the three universities. (Note that the sample sizes are not equal.) Use both the critical and p-value approaches.
(Essay)
4.8/5  (33)
(33)
Consider the following ANOVA table. 
The test statistic to test the null hypothesis equals
The test statistic to test the null hypothesis equals
(Multiple Choice)
4.8/5  (39)
(39)
The required condition for using an ANOVA procedure on data from several populations is that the
(Multiple Choice)
4.9/5  (28)
(28)
An ANOVA procedure is used for data obtained from five populations. Five samples, each comprised of 25 observations, were taken from the five populations. The numerator and denominator (respectively) degrees of freedom for the critical value of F are
(Multiple Choice)
4.8/5  (43)
(43)
An ANOVA procedure is applied to data obtained from 6 samples where each sample contains 20 observations. The critical value of F occurs with
(Multiple Choice)
4.8/5  (37)
(37)
In an analysis of variance, one estimate of σ2 is based upon the differences between the treatment means and the
(Multiple Choice)
4.7/5  (44)
(44)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 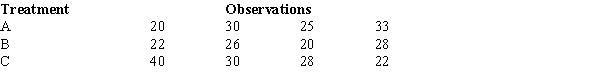
The test statistic to test the null hypothesis equals
The test statistic to test the null hypothesis equals
(Multiple Choice)
4.9/5  (28)
(28)
Which of the following is not a required assumption for the analysis of variance?
(Multiple Choice)
4.7/5  (39)
(39)
In a factorial experiment, if there are x levels of factor A and y levels of factor B, there is a total of
(Multiple Choice)
4.9/5  (35)
(35)
The process of using the same or similar experimental units for all treatments is called
(Multiple Choice)
4.8/5  (33)
(33)
For four populations, the population variances are assumed to be equal. Random samples from each population provide the following data. 
Using a .05 level of significance, test to see if the means for all four populations are the same.
Using a .05 level of significance, test to see if the means for all four populations are the same.
(Short Answer)
4.7/5  (30)
(30)
To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 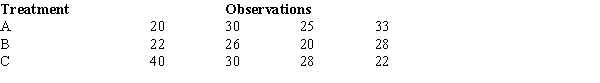 The mean square due to error (MSE) equals
The mean square due to error (MSE) equals
(Multiple Choice)
4.8/5  (35)
(35)
The process of allocating the total sum of squares and degrees of freedom to the various components is called
(Multiple Choice)
4.8/5  (39)
(39)
Part of an ANOVA table is shown below.  The mean square due to treatments (MSTR) is
The mean square due to treatments (MSTR) is
(Multiple Choice)
4.8/5  (42)
(42)
In an analysis of variance problem involving 3 treatments and 10 observations per treatment, SSE = 399.6. The MSE for this situation is
(Multiple Choice)
4.8/5  (36)
(36)
Consider the following information.
SSTR = 6750
H0: μ1 = μ2 = μ3 = μ4 =μ5
SSE = 8000
Ha: At least one mean is different
The null hypothesis is to be tested at the 5% level of significance. The null hypothesis
(Multiple Choice)
4.7/5  (23)
(23)
Showing 41 - 60 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)