Exam 23: Time-Series Analysis and Forecasting
Exam 1: What Is Statistics16 Questions
Exam 2: Types of Data, Data Collection and Sampling17 Questions
Exam 3: Graphical Descriptive Methods Nominal Data20 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures150 Questions
Exam 6: Probability112 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions118 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions68 Questions
Exam 11: Estimation: Describing a Single Population132 Questions
Exam 12: Estimation: Comparing Two Populations23 Questions
Exam 13: Hypothesis Testing: Describing a Single Population130 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations81 Questions
Exam 15: Inference About Population Variances47 Questions
Exam 16: Analysis of Variance125 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests116 Questions
Exam 18: Simple Linear Regression and Correlation219 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building100 Questions
Exam 21: Nonparametric Techniques136 Questions
Exam 22: Statistical Inference: Conclusion106 Questions
Exam 23: Time-Series Analysis and Forecasting146 Questions
Exam 24: Index Numbers27 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
Given the following time series, compute the seasonal (quarterly) indexes, using the four-quarter centred moving averages. Quarter 1993 1994 1995 1996 1997 1 62 48 50 43 57 2 51 45 46 39 32 3 53 44 46 37 31 4 46 37 42 32 29
(Essay)
4.9/5  (41)
(41)
A 5 period moving average will show less fluctuation than a 3 period moving average, for the same time series.
(True/False)
4.8/5  (34)
(34)
Random variation is one of the four different components of a time series. It is caused by irregular and unpredictable changes in a time series that are not caused by any other component. It tends to mask the existence of the other, more predictable components.
(True/False)
4.8/5  (38)
(38)
A company selling swimming goggles wants to analyze its Australian sales figures.
Time series forecasting with regression was used to generate Excel output to estimate trend and seasonal effects of the time series of Swimming goggle sales (in thousands of dollars) where the origin is the March Quarter 2000 and Q1 denotes sales in the March quarter, Q3 denotes sales in the September quarter and Q4 denotes sales in the December quarter. SUMMARV OUTPUT Regression Stotitics Multiple R 0.9460 R Square 0.8950 Adjusted RSquare 0.8864 Standard Error 3.7394 Observations 54
Sgnificance df S MS F F Regression 4 5837.596003 1459.4 104.3701 2.41949-23 Residual 49 685.1632564 13.9829 Total 53 6522.759259
Standard Upper Coefficients Error t Stat p-value Lower 95\% 95\% Intercept 3.0588 1.3331 2.2944 0.0261 0.3797 5.7378 0.2518 0.0327 7.7052 0.0000 0.1861 0.3175 1 12.4604 1.3897 8.9664 0.0000 9.6677 15.2530 3 1.1458 1.4721 0.7784 0.4401 -1.8124 4.1041 4 23.9121 1.4403 16.6025 0.0000 21.0177 26.8064 (a) Write out the regression equations for each of the four quarters.
(b) Sketch the four equations from part (a) on the same set of axes.
(c) Interpret the coefficients on all the indicator variables.
(c) All the indicator variables have positive coefficients. Is this surprising? Explain.
(Essay)
4.7/5  (35)
(35)
Regression analysis was used to develop the following equation from 60 observations of quarterly data: 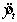 ,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise
Forecast the next four quarters.
,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise
Forecast the next four quarters.
(Essay)
4.8/5  (32)
(32)
A time series regression equation for a surfboard manufacturing company in Australia is given below: Y = 35 + 4Q1 + 0.5Q3 + 8Q4 + 3t
With t in quarters and the origin is December 2010 and Q1 is the indicator variable for March, Q3 is the indicator variable for September and Q4 is the indicator variable for December.
Which of the following statements is correct?
(Multiple Choice)
4.8/5  (35)
(35)
We calculate the five-period moving average for a time series for all time periods except the:
(Multiple Choice)
4.9/5  (49)
(49)
The following trend line was calculated from quarterly data for 2006-2010: ŷ = 2.35 + 0.12t, where t = 1 for the first quarter of 2006. The seasonal indexes computed from the trend line for the four quarters of the year 2011 are 0.88, 0.93, 1.04, and 1.17, respectively. The seasonalised forecast for the third quarter of the year 2011 is:
(Multiple Choice)
4.7/5  (30)
(30)
A time series regression equation measuring the number of surfboards sold by a surfboard manufacturing company in Australia is given below:
Y = 35 + 4Q1 + 0.5Q3 + 8Q4 + 3t
With t in quarters and the origin is December 2010 and Q1 is the indicator variable for March, Q3 is the indicator variable for September and Q4 is the indicator variable for December.
Which of the following statements is correct?
(Multiple Choice)
4.8/5  (31)
(31)
The time-series component that reflects the irregular changes in a time series that are not caused by any other component, and tends to hide the existence of the other, more predictable components, is called random variation.
(True/False)
4.8/5  (40)
(40)
Which of the following components of a time-series reflects the overall general movement of the data?
(Multiple Choice)
4.8/5  (31)
(31)
The trend equation for quarterly sales data (in millions of dollars) for 2001-2005 is 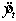 , where t = 1 for the first quarter of 2001. The seasonal index for the third quarter of 2006 is 1.25. The forecast sales for the third quarter of 2006 is:
, where t = 1 for the first quarter of 2001. The seasonal index for the third quarter of 2006 is 1.25. The forecast sales for the third quarter of 2006 is:
(Multiple Choice)
4.9/5  (43)
(43)
Quarterly enrolments in a business statistics class for three years are shown below. Year Quarter Enrolment 1996 1 26 2 29 3 33 4 18 1997 1 27 2 25 3 36 4 21 1 32 1998 2 36 3 39 4 30 Compute the four-quarter centred moving averages.
(Essay)
4.9/5  (35)
(35)
The purpose of using the moving average is to take away the short-term seasonal and random variation, leaving behind a combined trend and cyclical movement.
(True/False)
4.8/5  (31)
(31)
Time-series forecasting with exponential smoothing uses the following formula:` . where is the exponentially smoothed time series at time t, is the value of the time series at time t, and w is the smoothing constant. The forecast value at time t + 1, where w = 0.3, is given by:
(Multiple Choice)
4.8/5  (33)
(33)
If we wanted to measure the seasonal variations on stock market performance by month, we would need:
(Multiple Choice)
4.7/5  (38)
(38)
Of the four components of the multiplicative time-series model, the ratio of the time series to the moving average isolates the:
(Multiple Choice)
4.9/5  (41)
(41)
A time series is shown in the table below: Time period 1 48 2 50 3 46 4 42 5 40 6 32 7 34 8 26 9 21 10 13 a. Plot the time series to determine which of the trend models appears to fit better.
b. Use the regression technique to calculate the linear trend line and the quadratic trend line. Which line fits better? Use the best model to forecast the value of y for time period 7.
(Essay)
4.8/5  (34)
(34)
Showing 41 - 60 of 146
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)