Exam 23: Time-Series Analysis and Forecasting
Exam 1: What Is Statistics16 Questions
Exam 2: Types of Data, Data Collection and Sampling17 Questions
Exam 3: Graphical Descriptive Methods Nominal Data20 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures150 Questions
Exam 6: Probability112 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions118 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions68 Questions
Exam 11: Estimation: Describing a Single Population132 Questions
Exam 12: Estimation: Comparing Two Populations23 Questions
Exam 13: Hypothesis Testing: Describing a Single Population130 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations81 Questions
Exam 15: Inference About Population Variances47 Questions
Exam 16: Analysis of Variance125 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests116 Questions
Exam 18: Simple Linear Regression and Correlation219 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building100 Questions
Exam 21: Nonparametric Techniques136 Questions
Exam 22: Statistical Inference: Conclusion106 Questions
Exam 23: Time-Series Analysis and Forecasting146 Questions
Exam 24: Index Numbers27 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
Which of the following best describes what may be used when measuring the seasonal and random variation of a time series with no cyclical effect?
(Multiple Choice)
4.9/5  (33)
(33)
The time-series component that reflects a wavelike pattern describing a long-term trend that is generally apparent over a number of years is called seasonal.
(True/False)
4.8/5  (27)
(27)
The result of a quadratic model fit to time-series data was 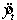 , where t = 1 for 1994. The forecast value for 2001 is 129.25.
, where t = 1 for 1994. The forecast value for 2001 is 129.25.
(True/False)
4.9/5  (30)
(30)
The total number of overtime hours (in 1000s) worked in a large steel mill was recorded for 16 quarters, as shown below. Year Quarter Overtime hours 2007 1 20 2 30 3 28 4 20 2008 1 24 2 34 3 28 4 21 2009 1 28 2 38 3 31 4 26 2010 1 30 2 41 3 35 4 28 a. Use the regression technique to calculate the linear trend line.
b. Calculate the seasonal indexes based on the regression trend line in part (a).
c. What do the seasonal indexes tell us?
(Essay)
4.9/5  (35)
(35)
The mean absolute deviation (MAD) and the sum of squares for forecast error (SSE) are the most commonly used measures of forecast accuracy. The model that forecasts the data best will usually have the:
(Multiple Choice)
4.8/5  (24)
(24)
Which of the following are examples of seasons when measuring the seasonal component of a time series?
(Multiple Choice)
4.9/5  (36)
(36)
The term 'seasonal variation' may refer to the four traditional seasons, or to systematic patterns that occur during a quarter, a week, or even one day, but within 12 months.
(True/False)
4.9/5  (42)
(42)
The table below shows the number of pizzas sold daily during a four-week period at King Pizza in Melbourne. Week Day 1 2 3 4 Sunday 253 234 248 232 Monday 98 93 99 104 Tuesday 106 88 87 115 Wednesday 119 134 113 102 Thursday 138 123 130 118 Friday 201 215 218 205 Saturday 327 399 415 390 a. Calculate the seasonal (daily) indexes, using a seven-day moving average.
b. Use regression analysis to find the linear trend line.
c. Calculate the seasonal (daily) indexes, using the trend line developed in (b).
(Essay)
4.8/5  (39)
(39)
The stock market has a 5-day working week. If we wanted to measure the impact of the day of the week on stock market performance, we would need:
(Multiple Choice)
4.9/5  (43)
(43)
The time-series component that reflects a long-term, relatively smooth pattern or direction exhibited by a time series over a long time period is called trend.
(True/False)
4.8/5  (38)
(38)
In determining weekly seasonal indexes for natural gas consumption, the sum of the 52 means for gas consumption as a percentage of the moving average is 5195. To get the seasonal indexes, each monthly mean is to be multiplied by (5200 / 5195).
(True/False)
4.9/5  (33)
(33)
Regression analysis with t = 1 to 40 was used to develop the following equation: 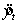 ,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four quarters.
,
where: = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four quarters.
(Essay)
4.9/5  (43)
(43)
A company selling swimming goggles wants to analyze the company's Australian sales figures.
Time series forecasting with regression was used to generate Excel output to estimate trend of the time series of Swimming goggle sales (in thousands of dollars) where the origin is the March Quarter 2000. SUMMARV OUTPUT Regression Stotitics Multiple R 0.37281 R Square 0.13899 Adjusted R Square 0.12243 StandardError 10.3925 Observations 54
Sgnificance df S MS F F Regression 1 906.5867925 906.59 8.39406 0.005497292 Residual 52 5616.172467 108 Total 53 6522.759259
Standard Upper Coefficients Error t Stat p-value Lower 95\% 95\% Intercept 12.237 2.789633876 4.3866 5.6-05 6.639227133 17.8348469 0.26289 0.090738795 2.8973 0.0055 0.080812368 0.4449738 (a) Forecast goggles sales for each quarter of 2016.
(b) Are these good predictions? Explain.
(Essay)
4.8/5  (34)
(34)
a. Apply exponential smoothing with w = 0.1 and w = 0.8 to help detect the components of the following time series. Period t y 1 40 2 45 3 44 4 47 5 48 6 50 7 52 8 51 9 48 10 47 b. Draw the time series and the two sets of exponentially smoothed values. Does there appear to be a trend component in the time series?
(Essay)
4.7/5  (24)
(24)
The actual and forecast values of a time series are shown below. Actual values Forecast values 135 140 162 165 155 150 182 191 174 168 194 190 233 220 280 240 a. Calculate the mean absolute deviation (MAD).
b. Calculate the sum of squares for forecast error (SSE).
(Essay)
4.8/5  (42)
(42)
Which of the following methods is appropriate for forecasting a time series when the trend, cyclical and seasonal components of the series are not significant?
(Multiple Choice)
4.7/5  (27)
(27)
A time series can consist of four different components: long-term trend, cyclical variation, seasonal variation, and random variation.
(True/False)
4.9/5  (36)
(36)
Regression analysis with t = 1 to 80 was used to develop the following forecast equation:
t = 135 + 4.8t -1.3Q1 -1.7Q2 + 1.5Q3
where:
Qi = 1, if quarter i (i = 1, 2, 3)
= 0, otherwise.
Forecast the next four values.
(Essay)
4.9/5  (39)
(39)
To calculate the five-period moving average of a time series for a given time period, we average the value in that time period and the values in the four preceding periods.
(True/False)
4.9/5  (35)
(35)
Of the four different components of a time series, cyclical variation is the one most likely to exhibit the long-term direction of the data.
(True/False)
4.8/5  (39)
(39)
Showing 101 - 120 of 146
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)