Question 1

Which of the following best describes the range of the coefficient of multiple determination?

Accepted Answer

A)  0 to 1 
B)  −1 to 1 
C)  1.0 to n, where n is the number of observations in the sample. 
D)  1 to k, where k is the number of independent variables in the model. 
A)  0 to 1 
B)  −1 to 1 
C)  1.0 to n, where n is the number of observations in the sample. 
D)  1 to k, where k is the number of independent variables in the model.

Question 2

A multiple regression model involves 5 independent variables and the sample size is 30. If we want to test the validity of the model at the 5% significance level, the critical value is:

Accepted Answer

A)  2.59. 
B)  2.53. 
C)  2.62. 
D)  2.56. 
A)  2.59. 
B)  2.53. 
C)  2.62. 
D)  2.56.

Question 3

In multiple regression with k independent variables, the t-tests of the individual coefficients allow us to determine whether $\beta _ { i } \neq 0$ (for i = 1, 2, …, k), which tells us whether a linear relationship exists between $x _ { i }$ and y.

Accepted Answer

A) True 
 B)False

Question 4

In multiple regression analysis involving 9 independent variables and 110 observations, the critical value of t for testing individual coefficients in the model will have:

Accepted Answer

A)  109 degrees of freedom. 
B)  8 degrees of freedom. 
C)  99 degrees of freedom. 
D)  100 degrees of freedom. 
A)  109 degrees of freedom. 
B)  8 degrees of freedom. 
C)  99 degrees of freedom. 
D)  100 degrees of freedom.

Question 5

To test the validity of a multiple regression model involving 2 independent variables, the null hypothesis is that:

Accepted Answer

A)  $\beta$0 = $\beta$1 = $\beta$2. 
B)  $\beta$0 = $\beta$1 = $\beta$2 = 0. 
C)  $\beta$1 = $\beta$2 = 0. 
D)  $\beta$1 = $\beta$2. 
A)  $\beta$0 = $\beta$1 = $\beta$2. 
B)  $\beta$0 = $\beta$1 = $\beta$2 = 0. 
C)  $\beta$1 = $\beta$2 = 0. 
D)  $\beta$1 = $\beta$2.

Question 6

Which of the following is used to test the significance of the overall regression equation?

Accepted Answer

A)  t-test.. 
B)  z-test. 
C)  χ2 test 
D)  F-test 
A)  t-test.. 
B)  z-test. 
C)  χ2 test 
D)  F-test

Question 7

In a multiple regression model, the standard deviation of the error variable $\varepsilon$ is assumed to be:

Accepted Answer

A)  constant for all values of the independent variables. 
B)  constant for all values of the dependent variable. 
C)  1.0. 
D)  None of these choices are correct. 
A)  constant for all values of the independent variables. 
B)  constant for all values of the dependent variable. 
C)  1.0. 
D)  None of these choices are correct.

Question 8

A multiple regression model has the form $\hat{y}$ = b0 + b1x1 + b2x2. The coefficient b2 is interpreted as the change in $y$ per unit change in x2.

Accepted Answer

A) True 
 B)False

Question 9

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $x _ { 3 }$ = mid-term test mark (out of 100).
The professor recorded the data for 50 randomly selected students. The computer output is shown below.
THE REGRESSION EQUATION IS 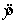  = $41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$ $$\begin{array} { | c | c c c | } 
\hline \text { Predictor } & \text { Coef } & \text { StDev } & \mathrm { T } \
\hline \text { Constant } & 41.6 & 17.8 & 2.337 \
x _ { 1 } & - 3.18 & 1.66 & - 1.916 \
x _ { 2 } & - 1.17 & 1.13 & - 1.035 \
x _ { 3 } & 0.63 & 0.13 & 4.846 \
\hline
\end{array}$$ S = 13.74 R-Sq = 30.0%. $$\begin{array}{l}
\text { ANALYSIS OF VARIANCE }\
\begin{array} { | l | c c c c | } 
\hline \text { Source of Variation } & \mathrm { df } & \text { SS } & \text { MS } & \text { F } \
\hline \text { Regression } & 3 & 3716 & 1238.667 & 6.558 \
\text { Error } & 46 & 8688 & 188.870 & \
\hline \text { Total } & 49 & 12404 & & \
\hline
\end{array}
\end{array}$$ Interpret the coefficients $b _ { 1 }$ and $b _ { 3 }$ .

Accepted Answer

@#IMG-DLM& = -3.18. This tells us that for each ad

Question 10

Given the multiple linear regression equation 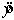 $= - 0.80 + 0.12 x _ { 1 } + 0.08 x _ { 2 }$ , the value -0.80 is the $y$ intercept.

Accepted Answer

A) True 
 B)False

Question 11

A multiple regression model has the form $\hat{y}$ = 24 - 0.001x1 + 3x2.
As x1 increases by 1 unit, holding $x _ { 2 }$ constant, the value of y is estimated to decrease by 0.001units, on average.

Accepted Answer

A) True 
 B)False

Question 12

In multiple regression, and because of a commonly occurring problem called multicollinearity, the
t-tests of the individual coefficients may indicate that some independent variables are not linearly related to the dependent variable, when in fact they are.

Accepted Answer

A) True 
 B)False

Question 13

Which of the following best explains a small F-statistic when testing the validity of a multiple regression model?

Accepted Answer

A)  Most of the variation in x is unexplained by the regression equation. 
B)  Most of the variation in y is explained by the regression equation. 
C)  The model provides a good fit. 
D)  Most of the variation in y is unexplained by the regression equation. 
A)  Most of the variation in x is unexplained by the regression equation. 
B)  Most of the variation in y is explained by the regression equation. 
C)  The model provides a good fit. 
D)  Most of the variation in y is unexplained by the regression equation.

Question 14

A statistician wanted to determine whether the demographic variables of age, education and income influence the number of hours of television watched per week. A random sample of 25 adults was selected to estimate the multiple regression model $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = number of hours of television watched last week. $x _ { 1 }$ = age. $x _ { 2 }$ = number of years of education. $x _ { 3 }$ = income (in $1000s).
The computer output is shown below.
THE REGRESSION EQUATION IS $$y =$$ $$22.3 + 0.41 x _ { 1 } - 0.29 x _ { 2 } - 0.12 x _ { 3 }$$ $$\begin{array} { | c | c c c | } 
\hline \text { Predictor } & \text { Coef } & \text { StDev } & \mathrm { T } \
\hline \text { Constant } & 22.3 & 10.7 & 2.084 \
x _ { 1 } & 0.41 & 0.19 & 2.158 \
x _ { 2 } & - 0.29 & 0.13 & - 2.231 \
x _ { 3 } & - 0.12 & 0.03 & - 4.00 \
\hline
\end{array}$$ S = 4.51 R-Sq = 34.8%. $$\begin{array}{l}
\text { ANALYSIS OF VARIANCE }\
\begin{array} { | l | c c c c | } 
\hline \text { Source of Variation } & \text { df } & \text { SS } & \text { MS } & \text { F } \
\hline \text { Regression } & 3 & 227 & 75.667 & 3.730 \
\text { Error } & 21 & 426 & 20.286 & \
\hline \text { Total } & 24 & 653 & & \
\hline
\end{array}
\end{array}$$ Test the overall validity of the model at the 5% significance level.

Accepted Answer

@#IMG-DLM& . @#IMG-DLM& At least one @#IMG-DLM& is not equal

Question 15

In a multiple regression analysis involving 4 independent variables and 30 data points, the number of degrees of freedom associated with the sum of squares for error, SSE, is 25.

Accepted Answer

A) True 
 B)False

Question 16

A multiple regression analysis that includes 25 data points and 4 independent variables produces SST = 400 and SSR = 300. The multiple standard error of estimate will be 5.

Accepted Answer

A) True 
 B)False

Question 17

Excel and Minitab print a second $R ^ { 2 }$ statistic, called the coefficient of determination adjusted for degrees of freedom, which has been adjusted to take into account the sample size and the number of independent variables.

Accepted Answer

A) True 
 B)False

Question 18

In regression analysis, the total variation in the dependent variable y, measured by $\sum \left( y _ { i } - \bar { y } \right) ^ { 2 }$ , can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.

Accepted Answer

A) True 
 B)False

Question 19

Pop-up coffee vendors have been popular in the city of Adelaide in 2013. A vendor is interested in knowing how temperature (in degrees Celsius) and number of different pastries and biscuits offered to customers impacts daily hot coffee sales revenue (in $00's).
A random sample of 6 days was taken, with the daily hot coffee sales revenue and the corresponding temperature and number of different pastries and biscuits offered on that day, noted.
Excel output for a multiple linear regression is given below: $$\begin{array} { | c | c | r | } 
\hline \text { Coffee sales revenue } & \text { Temperature } & \text { Pastries/biscuits } \
\hline 6.5 & 25 & 7 \
\hline 10 & 17 & 13 \
\hline 5.5 & 30 & 5 \
\hline 4.5 & 35 & 6 \
\hline 3.5 & 40 & 3 \
\hline 28 & 9 & 15 \
\hline
\end{array}$$ \(\begin{array}{|l|r|r|r|r|r|c|}\hline \text { SUMMARV } \
\text { OUTPUT } \
\hline \text { Regression } \
\text { Stotistics } \
\hline \text { Multiple R } & 0.87 \
\hline \text { R Square } & 0.75 \
\hline \begin{array}{l}
\text { Adjusted R } \
\text { Square }
\end{array} & 0.59 \
\hline \text { Standard Error } & 5.95 \
\hline \text { Otservations } & 6.00 \
\hline\
\hline \text { ANOVA }\
\hline & & & & & \text { Significonce } \
& \text { df } & S S & M S & F & F \
\hline \text { Regression } & 2.00 & 322.14 & 161.07 & 4.55 & 0.12 \\hline \text { Residual } & 3.00 & 106.20 & 35.40 \
\hline \text { Total } & 5.00 & 428.33 & \
\hline\
\hline & \text { Coefficients } & {\begin{array}{c}
\text { Standard } \
\text { Error }
\end{array}} & {\text { tStot }} & \text { Pvolue } & \text { Lower 95\% } & \begin{array}{c}
\text { Upper } \
95 \%
\end{array} \
\hline \text { Intercept } & 18.68 & 37.8 & 0.49 & 0.66 & -101.88 & 139.24 \
\hline \text { Temperature } & -0.50 & 0.83 & -0.60 & 0.59 & -3.15 & 2.15 \
\hline \text { Patries/bisouits } & 0.49 & 2.02 & 0.24 & 0.82 & -5.94 & 6.92 \
\hline
\end{array}\) Interpret the intercept. Does this make sense?

Accepted Answer

We estimate that if the temperature were

Question 20

The multiple coefficient of determination is defined as:

Accepted Answer

A)  SSE/SSY. 
B)  MSE/MSR. 
C)  1 - (SSE/SSY). 
D)  1 - (MSE/MSR). 
A)  SSE/SSY. 
B)  MSE/MSR. 
C)  1 - (SSE/SSY). 
D)  1 - (MSE/MSR).

Exam 19: Multiple Regression

Which of the following best describes the range of the coefficient of multiple determination?

A multiple regression model involves 5 independent variables and the sample size is 30. If we want to test the validity of the model at the 5% significance level, the critical value is:

In multiple regression with k independent variables, the t-tests of the individual coefficients allow us to determine whether βi≠0\beta _ { i } \neq 0βi​=0 (for i = 1, 2, …, k), which tells us whether a linear relationship exists between xix _ { i }xi​ and y.

In multiple regression analysis involving 9 independent variables and 110 observations, the critical value of t for testing individual coefficients in the model will have:

To test the validity of a multiple regression model involving 2 independent variables, the null hypothesis is that:

Which of the following is used to test the significance of the overall regression equation?

In a multiple regression model, the standard deviation of the error variable ε\varepsilonε is assumed to be:

A multiple regression model has the form y^\hat{y}y^​ = b0 + b1x1 + b2x2. The coefficient b2 is interpreted as the change in yyy per unit change in x2.

Given the multiple linear regression equation =−0.80+0.12x1+0.08x2= - 0.80 + 0.12 x _ { 1 } + 0.08 x _ { 2 }=−0.80+0.12x1​+0.08x2​ , the value -0.80 is the yyy intercept.

A multiple regression model has the form y^\hat{y}y^​ = 24 - 0.001x1 + 3x2. As x1 increases by 1 unit, holding x2x _ { 2 }x2​ constant, the value of y is estimated to decrease by 0.001units, on average.

In multiple regression, and because of a commonly occurring problem called multicollinearity, the t-tests of the individual coefficients may indicate that some independent variables are not linearly related to the dependent variable, when in fact they are.

Which of the following best explains a small F-statistic when testing the validity of a multiple regression model?

In a multiple regression analysis involving 4 independent variables and 30 data points, the number of degrees of freedom associated with the sum of squares for error, SSE, is 25.

A multiple regression analysis that includes 25 data points and 4 independent variables produces SST = 400 and SSR = 300. The multiple standard error of estimate will be 5.

Excel and Minitab print a second R2R ^ { 2 }R2 statistic, called the coefficient of determination adjusted for degrees of freedom, which has been adjusted to take into account the sample size and the number of independent variables.

In regression analysis, the total variation in the dependent variable y, measured by ∑(yi−yˉ)2\sum \left( y _ { i } - \bar { y } \right) ^ { 2 }∑(yi​−yˉ​)2 , can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.

The multiple coefficient of determination is defined as:

What Is Statistics

Types of Data, Data Collection and Sampling

Graphical Descriptive Methods Nominal Data

Graphical Descriptive Techniques Numerical Data

Numerical Descriptive Measures

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Statistical Inference: Introduction

Sampling Distributions

Estimation: Describing a Single Population

Estimation: Comparing Two Populations

Hypothesis Testing: Describing a Single Population

Hypothesis Testing: Comparing Two Populations

Inference About Population Variances

Analysis of Variance

Additional Tests for Nominal Data: Chi-Squared Tests

Simple Linear Regression and Correlation

Model Building

Nonparametric Techniques

Statistical Inference: Conclusion

Time-Series Analysis and Forecasting

Index Numbers

Decision Analysis

Filters

In multiple regression with k independent variables, the t-tests of the individual coefficients allow us to determine whether $\beta _ { i } \neq 0$ (for i = 1, 2, …, k), which tells us whether a linear relationship exists between $x _ { i }$ and y.

In a multiple regression model, the standard deviation of the error variable $\varepsilon$ is assumed to be:

A multiple regression model has the form $\hat{y}$ = b₀+ b₁x₁ + b₂x₂. The coefficient b₂ is interpreted as the change in $y$ per unit change in x₂.

Given the multiple linear regression equation $Given the multiple linear regression equation = - 0.80 + 0.12 x _ { 1 } + 0.08 x _ { 2 } , the value -0.80 is the y intercept.$ $= - 0.80 + 0.12 x _ { 1 } + 0.08 x _ { 2 }$ , the value -0.80 is the $y$ intercept.

A multiple regression model has the form $\hat{y}$ = 24- 0.001x₁ + 3x₂. As x₁ increases by 1 unit, holding $x _ { 2 }$ constant, the value of y is estimated to decrease by 0.001units, on average.

Excel and Minitab print a second $R ^ { 2 }$ statistic, called the coefficient of determination adjusted for degrees of freedom, which has been adjusted to take into account the sample size and the number of independent variables.

In regression analysis, the total variation in the dependent variable y, measured by $\sum \left( y _ { i } - \bar { y } \right) ^ { 2 }$ , can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.