Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management
It is improper to combine manufacturing costs and overtime costs in the same objective function.
False
Target Shirt Company makes three varieties of shirts: Collegiate, Traditional and European. These shirts are made from different combinations of cotton and polyester.
?
The cost per yard of unblended cotton is $5 and for unblended polyester is $4. Target can receive up to 4,000 yards of raw cotton and 3,000 yards of raw polyester fabric weekly. The table below pertinent data concerning the manufacture of the shirts.
? 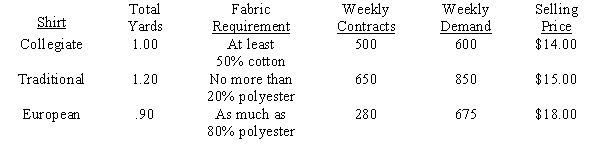 ?
Formulate and solve this blending problem as a linear program.
?
Formulate and solve this blending problem as a linear program.
?
Formulation
Decision variables
Not only must we decide how many shirts to make and how much fabric to purchase, we also need to decide how much of each fabric is blended into each shirt.
?
Let, sj = the total number of shirt style j produced
fi = the number of yards of material i purchased
xij = yards of fabric i blended into shirt style j
where i = 1 (cotton) or 2 (polyester) and
j = 1 (collegiate), 2(traditional), or 3 (European)?
Objective function
Maximize the overall profit.
To determine the profit function, subtract the cost of purchasing the fabric from the shirt sales revenue. Thus the objective function is:
?
Max 14s1 + 15s2 + 18s3 - 5f1 - 4f2
?
Constraints
Definition of Total Number of Shirts of Each Style
Total Number of each style =
(Total Yardage used in making the style) / (Yardage/Shirt)(1) Collegiate: s1 = (x11 + x21) / 1 >>> s1 - x11 - x21 = 0
(2) Traditional: s2 = (x12 + x22) / 1.2 >>> 1.2s2 - x12 - x22 = 0
(3) European: s3 = (x13 + x23) / .9 >>> .95s3 -x13 -x23 = 0
?
Definition of Total Yardage of Materials
(4) Cotton: f1 = x11 + x12 + x13 >>> f1 - x11 - x12 - x13 = 0
(5) Polyester: f2 = x21 + x22 + x23 >>> f2 - x21 - x22 - x23 = 0
?
Weekly Availability of the Resources
(6) Cotton: f1 < 4000
(7) Polyester: f2 < 3000
?
Meet Weekly Contracts
(8) Collegiate: s1 > 500
(9) Traditional: s2 > 650
(10) European: s3 > 280
?
Do Not Exceed Weekly Demand
(11) Collegiate: s1 < 600
(12) Traditional: s2 < 850
(13) European: s3 < 675
?
Fabric Requirements
Collegiate At Least 50% Cotton:
(Total yds. of Cotton in Colleg. Shirts) > [(.5(1.00) yds./shirt)(number of colleg. shirts)]
(14) x11 > .5s1 >>> x11 -.5s1 > 0
?
Traditional At Most 20% Polyester:
(Total yds. Polyester in Tradit. Shirts) < [.2(1.20) yds./shirt)(number of tradit. shirts)]
(15) x22 < .24s2 >>> x22 -.24s2 < 0
?
European At Most 80% Polyester:
(Total yds. Polyester in Europ. Shirts) < [.8(.90) yds./shirt)(number of Europ. shirts)]
(16) x23 < .72s3 >>> x23 - .72s3 < 0
?
Nonnegativity of variables
sj, fi, xij > 0 for i = 1,2 and j = 1,2,3.
?
Solution
Total profit = $23,152.50
Cotton collegiate yds. = 300.0, cotton traditional yds. = 816.0, cotton European yds. = 121.5,
polyester collegiate yds. = 300.0, polyester traditional yds. = 204.0, polyester European yds = 486.0, collegiate shirts = 600, traditional shirts = 850, European shirts = 675, cotton yards = 1237.5, polyester yards = 990.0
If Pij = the production of product i in period j, then to indicate that the limit on production of the company's three products in period 2 is 400,
B
The marketing research model presented in the textbook involves minimizing total interview cost subject to interview quota guidelines.
John Sweeney is an investment advisor who is attempting to construct an "optimal portfolio" for a client who has $400,000 cash to invest. There are ten different investments, falling into four broad categories that John and his client have identified as potential candidates for this portfolio.
The following table lists the investments and their important characteristics. Note that Unidyde Equities (stocks) and Unidyde Debt (bonds) are two separate investments, whereas First General REIT is a single investment that is considered both an equities and a real estate investment. 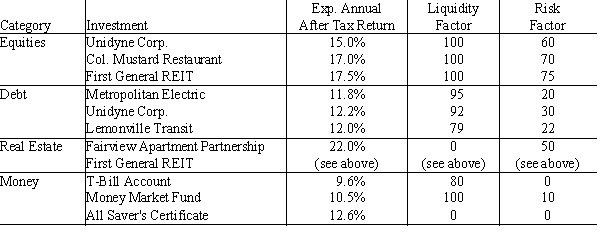
Formulate and solve a linear program to accomplish John's objective as an investment advisor which is to construct a portfolio that maximizes his client's total expected after-tax return over the next year, subject to a number of constraints placed upon him by the client for the portfolio:
1.Its (weighted) average liquidity factor must be at least 65.
2.The (weighted) average risk factor must be no greater than 55.
3.At most, $60,000 is to be invested in Unidyde stocks or bonds.
4.No more than 40% of the investment can be in any one category except the money category.
5.No more than 20% of the investment can be in any one investment except the money market fund.
6.At least $1,000 must be invested in the money market fund.
7.The maximum investment in All Saver's Certificates is $15,000.
8.The minimum investment desired for debt is $90,000.
9.At least $10,000 must be placed in a T-Bill account.
Formulate and solve a linear program to accomplish John's objective as an investment advisor which is to construct a portfolio that maximizes his client's total expected after-tax return over the next year, subject to a number of constraints placed upon him by the client for the portfolio:
1.Its (weighted) average liquidity factor must be at least 65.
2.The (weighted) average risk factor must be no greater than 55.
3.At most, $60,000 is to be invested in Unidyde stocks or bonds.
4.No more than 40% of the investment can be in any one category except the money category.
5.No more than 20% of the investment can be in any one investment except the money market fund.
6.At least $1,000 must be invested in the money market fund.
7.The maximum investment in All Saver's Certificates is $15,000.
8.The minimum investment desired for debt is $90,000.
9.At least $10,000 must be placed in a T-Bill account.
Data collection for large-scale LP models can be more time-consuming than either the formulation of the model or the development of the computer solution.
To study consumer characteristics, attitudes, and preferences, a company would engage in
Tots Toys makes a plastic tricycle that is composed of three major components: a handlebar-front wheel-pedal assembly, a seat and frame unit, and rear wheels. The company has orders for 12,000 of these tricycles. Current schedules yield the following information.  The company obviously does not have the resources available to manufacture everything needed for the completion of 12000 tricycles so has gathered purchase information for each component. Develop a linear programming model to tell the company how many of each component should be manufactured and how many should be purchased in order to provide 12000 fully completed tricycles at the minimum cost.
The company obviously does not have the resources available to manufacture everything needed for the completion of 12000 tricycles so has gathered purchase information for each component. Develop a linear programming model to tell the company how many of each component should be manufactured and how many should be purchased in order to provide 12000 fully completed tricycles at the minimum cost.
Why should decision makers who are primarily concerned with marketing or finance or production know about linear
programming?
Compared to the problems in the textbook, real-world problems generally require more variables and constraints.
A mutual fund manager must decide how much money to invest in Atlantic Oil (A) and how much to invest in Pacific Oil (P). At least 60% of the money invested in the two oil companies must be in Pacific Oil. A correct modeling of this constraint is
Portfolio selection problems should acknowledge both risk and return.
Discuss at least three additional considerations that might be included in media selection LP models more complex
than the one covered in the text.
A marketing research application uses the variable HD to represent the number of homeowners interviewed during the day. The objective function minimizes the cost of interviewing this and other categories and there is a constraint that HD ≥ 100. The solution indicates that interviewing another homeowner during the day will increase costs by 10.00. What do you know?
Using minutes as the unit of measurement on the left-hand side of a constraint and using hours on the right-hand side is acceptable since both are a measure of time.
The Tots Toys Company is trying to schedule production of two very popular toys for the next three months: a rocking horse and a scooter. Information about both toys is given below. 
 Develop a model that would tell the company how many of each toy to produce during each month. You are to minimize total cost. Inventory cost will be levied on any items in inventory on June 30, July 31, or August 31 after demand for the month has been satisfied. Your model should make use of the relationship
Beginning Inventory + Production − Demand = Ending Inventory
for each month. The company wants to end the summer with 150 rocking horses and 60 scooters as beginning inventory for Sept. 1. Don't forget to define your decision variables.
Develop a model that would tell the company how many of each toy to produce during each month. You are to minimize total cost. Inventory cost will be levied on any items in inventory on June 30, July 31, or August 31 after demand for the month has been satisfied. Your model should make use of the relationship
Beginning Inventory + Production − Demand = Ending Inventory
for each month. The company wants to end the summer with 150 rocking horses and 60 scooters as beginning inventory for Sept. 1. Don't forget to define your decision variables.
Wes Wheeler is the production manager of Wheeler Wheels, Inc. Wes has just received orders for 1,000 standard wheels and 1,250 deluxe wheels next month and for 800 standard and 1,500 deluxe wheels the following month. All orders are to be filled.
The cost of producing standard wheels is $10 and deluxe wheels is $16. Overtime rates are 50% higher. There are 1,000 hours of regular time and 500 hours of overtime available each month. It takes .5 hour to make a standard wheel and .6 hour to make a deluxe wheel. The cost of storing one wheel from one month to the next is $2.
Wes wants to develop a two-month production schedule for standard and deluxe wheels. Formulate this production planning problem as a linear program.
The media selection model presented in the textbook involves maximizing the number of potential customers reached subject to a minimum total exposure quality rating.
A&C Distributors is a company that represents many outdoor products companies and schedules deliveries to discount stores, garden centers, and hardware stores. Currently, scheduling needs to be done for two lawn sprinklers, the Water Wave and Spring Shower models. Requirements for shipment to a warehouse for a national chain of garden centers are shown below. 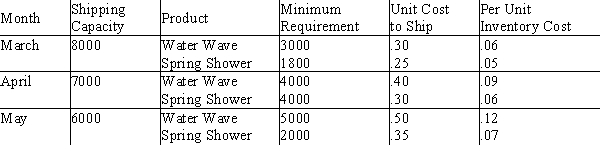 Let Sij be the number of units of sprinkler i shipped in month j, where i = 1 or 2, and j = 1, 2, or 3. Let Wij be the number of sprinklers that are at the warehouse at the end of a month, in excess of the minimum requirement.
a
Write the portion of the objective function that minimizes shipping costs.
b.An inventory cost is assessed against this ending inventory. Give the portion of the objective function that represents inventory cost.
c.There will be three constraints that guarantee, for each month, that the total number of sprinklers shipped will not exceed the shipping capacity. Write these three constraints.
d.There are six constraints that work with inventory and the number of units shipped, making sure that enough sprinklers are shipped to meet the minimum requirements. Write these six constraints.
Let Sij be the number of units of sprinkler i shipped in month j, where i = 1 or 2, and j = 1, 2, or 3. Let Wij be the number of sprinklers that are at the warehouse at the end of a month, in excess of the minimum requirement.
a
Write the portion of the objective function that minimizes shipping costs.
b.An inventory cost is assessed against this ending inventory. Give the portion of the objective function that represents inventory cost.
c.There will be three constraints that guarantee, for each month, that the total number of sprinklers shipped will not exceed the shipping capacity. Write these three constraints.
d.There are six constraints that work with inventory and the number of units shipped, making sure that enough sprinklers are shipped to meet the minimum requirements. Write these six constraints.
Media selection problems can maximize exposure quality and use number of customers reached as a constraint, or maximize the number of customers reached and use exposure quality as a constraint.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)