Exam 17: Linear Programming: Simplex Method
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Given the following initial simplex tableau 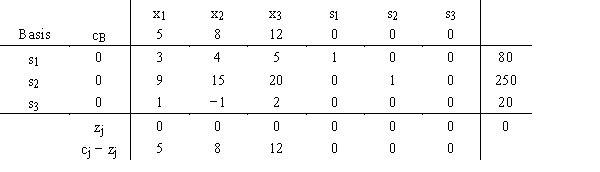
a.What variables form the basis?
b.What are the current values of the decision variables?
c.What is the current value of the objective function?
d.Which variable will be made positive next, and what will its value be?Which variable that is currently positive will become 0?
f.What value will the objective function have next?
a.What variables form the basis?
b.What are the current values of the decision variables?
c.What is the current value of the objective function?
d.Which variable will be made positive next, and what will its value be?Which variable that is currently positive will become 0?
f.What value will the objective function have next?
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
a.s1, s2 , s3
B.x1 = 0, x2 = 0, x3 = 0, s1 = 80, s2 = 250, s3 = 20
C.0
D.x3, 10
E.s3
F.z = 120
The purpose of the tableau form is to provide
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
C
If a variable is not in the basis, its value is 0.
Free
(True/False)
4.8/5  (34)
(34)
Correct Answer:
True
A simplex table is shown below. 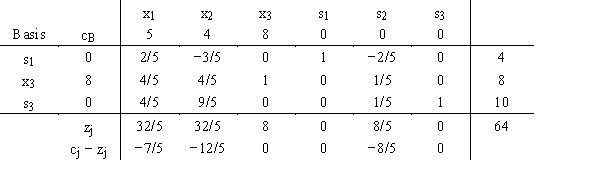
a.What is the current complete solution?
b.The 32/5 for z1 is composed of 0 + 8(4/5) + 0. Explain the meaning of this number.
c.Explain the meaning of the −12/5 value for c 2 − z2.
a.What is the current complete solution?
b.The 32/5 for z1 is composed of 0 + 8(4/5) + 0. Explain the meaning of this number.
c.Explain the meaning of the −12/5 value for c 2 − z2.
(Essay)
4.8/5  (35)
(35)
Coefficients in a nonbasic column in a simplex tableau indicate the amount of decrease in the current basic variables when the value of the nonbasic variable is increased from 0 to 1.
(True/False)
4.9/5  (40)
(40)
The purpose of row operations is to create a unit column for the entering variable while maintaining unit columns for the remaining basic variables.
(True/False)
4.9/5  (36)
(36)
A simplex tableau is shown below. 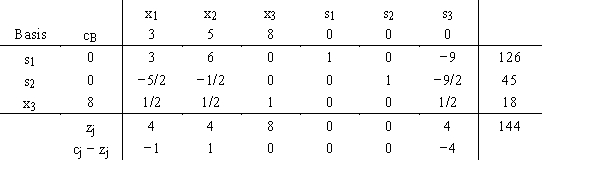
a.
Do one more iteration of the simplex procedure.
b.
What is the current complete solution?
c.
Is this solution optimal? Why or why not?
a.
Do one more iteration of the simplex procedure.
b.
What is the current complete solution?
c.
Is this solution optimal? Why or why not?
(Essay)
4.8/5  (39)
(39)
To determine a basic solution set of n−m, the variables equal to zero and solve the m linear constraint equations for the remaining m variables.
(True/False)
4.9/5  (42)
(42)
The basic solution to a problem with three equations and four variables would assign a value of 0 to
(Multiple Choice)
4.9/5  (26)
(26)
Algebraic methods such as the simplex method are used to solve
(Multiple Choice)
4.8/5  (42)
(42)
A solution is optimal when all values in the cj − zj row of the simplex tableau are either zero or positive.
(True/False)
4.9/5  (39)
(39)
For each of the special cases of infeasibility, unboundedness, and alternate optimal solutions, tell what you would do next with your linear programming model if the case occurred.
(Essay)
4.8/5  (42)
(42)
When there is a tie between two or more variables for removal from the simplex tableau,
(Multiple Choice)
4.9/5  (44)
(44)
In a simplex tableau, there is a variable associated with each column and both a constraint and a basic variable associated with each row.
(True/False)
4.9/5  (34)
(34)
Solve the following problem by the simplex method.
Max
14x1 + 14.5x2 + 18x3
s.t.
x1 + 2x2 + 2.5x3 ≤ 50
x1 + x2 + 1.5x3 ≤ 30
x1 , x2 , x3 ≥ 0
(Essay)
4.7/5  (35)
(35)
Write the following problem in tableau form. Which variables would be in the initial basic solution?
Min Z =
3x1 + 8x2
s.t.
x1 + x2 ≤ 200
x1 ≤ 80
x2 ≤ 60
(Essay)
4.7/5  (31)
(31)
A student in a Management Science class developed this initial tableau for a maximization problem and
now wants to perform row operations to obtain the next tableau and check for an optimal solution.
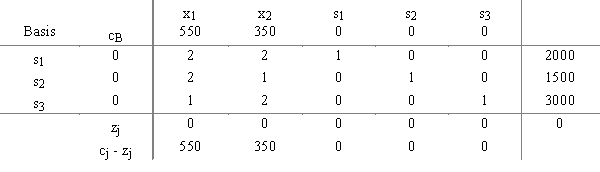
(Essay)
4.8/5  (38)
(38)
Showing 1 - 20 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)