Exam 20: Minimal Spanning Tree
What is a greedy algorithm? What is an example of a greedy algorithm?
A greedy algorithm is a simple, intuitive algorithmic paradigm that follows the problem-solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum. In other words, a greedy algorithm makes the best immediate, or "greedy," decision at every step, choosing the most beneficial option right now without considering the broader consequences. It assumes that by choosing a local optimum at each step, the final solution will also be optimal or close to optimal.
Greedy algorithms are used when a problem exhibits the following two properties:
1. Greedy Choice Property: A global optimum can be arrived at by making a locally optimal (greedy) choice.
2. Optimal Substructure: An optimal solution to the problem contains an optimal solution to subproblems.
However, greedy algorithms do not always yield the globally optimal solution for all problems because they usually do not consider the bigger picture. They are best suited for problems where choosing locally optimal also leads to a global optimum.
**Example of a Greedy Algorithm:**
One classic example of a greedy algorithm is the coin change problem, where the goal is to make change for a particular amount of cents using the least number of coins possible. Assume you have coins of denominations 1, 5, 10, and 25 cents, and you need to give change for 63 cents. A greedy algorithm would start by selecting the largest denomination less than or equal to the remaining amount, which is 25 cents in this case. It would then subtract this value from the total amount and repeat the process with the remaining amount. The steps would be as follows:
1. Choose a 25-cent coin: 63 - 25 = 38 cents remaining.
2. Choose another 25-cent coin: 38 - 25 = 13 cents remaining.
3. Choose a 10-cent coin: 13 - 10 = 3 cents remaining.
4. Choose three 1-cent coins: 3 - 3 = 0 cents remaining.
So, the greedy algorithm would use two 25-cent coins, one 10-cent coin, and three 1-cent coins, for a total of six coins.
This greedy strategy works because the coin denominations in the United States (and many other countries) are canonical, meaning that the greedy algorithm will always produce an optimal solution. However, if the coin denominations were different, such as 1, 3, and 4 cents, the greedy algorithm might not yield an optimal solution. For example, to make 6 cents, the greedy algorithm would choose one 4-cent coin and two 1-cent coins, for a total of three coins, whereas the optimal solution is two 3-cent coins.
Describe three examples of minimal spanning tree problems.
1. Network Design: When designing a communication network, such as a computer network or a transportation network, it is important to find the most efficient way to connect all the nodes while minimizing the total cost. This can be modeled as a minimal spanning tree problem, where the nodes represent the locations and the edges represent the connections between them.
2. Power Grid Optimization: In the field of electrical engineering, the problem of optimizing a power grid involves finding the most cost-effective way to connect power stations to consumers while ensuring that all areas are adequately supplied with electricity. This problem can be solved using minimal spanning tree algorithms to minimize the total length of power lines needed.
3. Cable TV Network: When laying down cable TV infrastructure, it is important to connect all the households to the main distribution center in the most efficient way possible. This can be formulated as a minimal spanning tree problem, where the households are the nodes and the connections between them are the edges, and the goal is to minimize the total length of cable needed.
The minimal spanning tree algorithm is considered to be:
A
Consider a minimal spanning tree problem in which pipe must be laid to connect sprinklers on a golf course. When represented with a network,
It is possible for minimal spanning tree problems to have alternative optimal solutions.
The arcs in a minimal spanning tree problem can be measured in terms of criteria other than distance.
The numbers on this network represent times to distribute a message. Use the minimal spanning tree algorithm to determine how messages should be passed in order to minimize total time.
 1. (River-1),(1-4),(4-6),(4-5),(6-7),(4-3),(3-8),(3-2).
2. (River-1),(1-4),(4-6),(4-5),(6-7),(4-3),(3-8),(4-2).
Total yards = 2050.
19.
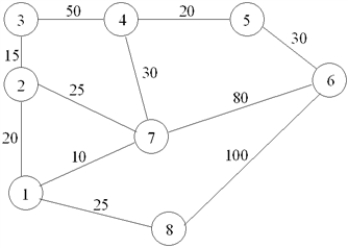
Griffith's Cherry Preserve is a combination wild animal habitat and amusement park. Besides their phenomenally successful wild animal safari tour, there are eight different theme areas in the amusement park.
One problem encountered by management is to develop a method by which people can efficiently travel between each area of the park. Management has learned that a people mover can be constructed at a cost of $50 per foot.
If the following network represents the distances (in feet) between each area of the park for which a people mover is possible, determine the minimum cost for such a system.
1. (River-1),(1-4),(4-6),(4-5),(6-7),(4-3),(3-8),(3-2).
2. (River-1),(1-4),(4-6),(4-5),(6-7),(4-3),(3-8),(4-2).
Total yards = 2050.
19.
Griffith's Cherry Preserve is a combination wild animal habitat and amusement park. Besides their phenomenally successful wild animal safari tour, there are eight different theme areas in the amusement park.
One problem encountered by management is to develop a method by which people can efficiently travel between each area of the park. Management has learned that a people mover can be constructed at a cost of $50 per foot.
If the following network represents the distances (in feet) between each area of the park for which a people mover is possible, determine the minimum cost for such a system.
The minimum spanning tree allows a person to visit every node without backtracking.
In the minimal spanning tree algorithm, you must consider the unconnected nodes that can be reached from any of the connected nodes, rather than arbitrarily considering only one of the connected nodes.
The minimal spanning tree algorithm will lead to an optimal solution regardless of which node is chosen at the start of the algorithm.
What are some other criteria (measures), besides distance, that might be minimized in a minimal spanning tree problem? Provide an example situation for each criterion.
For a network consisting of N nodes, a minimal spanning tree will consist of:
Cases in which a greedy algorithm provides the optimal solution are rare.
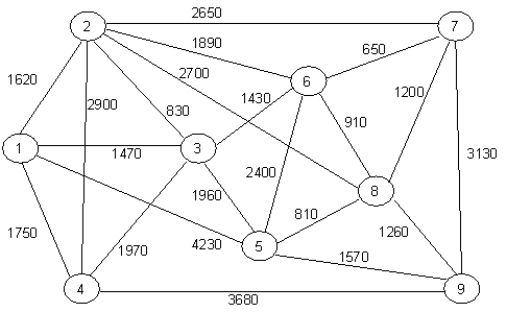
For the following eight cities with the given distances, find the minimal spanning tree path. 
The minimal spanning tree algorithm has connected nodes 8 and 9. Node 8 could be connected to nodes 11 (distance 6) and 12 (distance 5) and node 9 could be connected to node 12 (distance 3) and node 13 (distance 2). Which will you do next?
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)