Exam 2: An Introduction to Linear Programming
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Find the complete optimal solution to this linear programming problem.
Min
3X + 3Y
s.t.
12X + 4Y ≥ 48
10X + 5Y ≥ 50
4X + 8Y ≥ 32
X , Y ≥ 0
Free
(Essay)
4.9/5  (38)
(38)
Correct Answer:
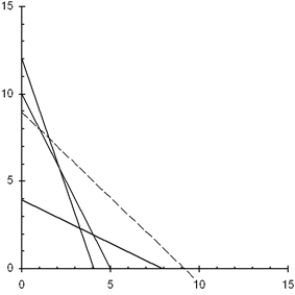
The complete optimal solution is X = 4, Y = 2, Z = 18, S1 = 8, S2 = 0, S3 = 0
Consider the following linear program:
Max
60X + 43Y
s.t.
X + 3Y ≥ 9
6X − 2Y = 12
X + 2Y ≤ 10
X, Y ≥ 0
a.
Write the problem in standard form.
b.
What is the feasible region for the problem?
c.
Show that regardless of the values of the actual objective function coefficients, the optimal solution will occur at one of two points. Solve for these points and then determine which one maximizes the current objective function.
Free
(Essay)
4.8/5  (29)
(29)
Correct Answer:
a.Max
60X + 43Y
s.t.
X + 3Y − S1 = 9
6X − 2Y = 12
X + 2Y + S3 = 10
X, Y, S1, S3 ≥ 0
B.Line segment of 6X − 2Y = 12 between (22/7,24/7) and (27/10,21/10).
C.Extreme points: (22/7,24/7) and (27/10,21/10). First one is optimal, giving Z = 336.
As long as the slope of the objective function stays between the slopes of the binding constraints
Free
(Multiple Choice)
4.8/5  (44)
(44)
Correct Answer:
C
All linear programming problems have all of the following properties EXCEPT
(Multiple Choice)
4.7/5  (36)
(36)
Consider the following linear programming problem
Max
8X + 7Y
s.t.
15X + 5Y ≤ 75
10X + 6Y ≤ 60
X + Y ≤ 8
X, Y ≥ 0
a.Use a graph to show each constraint and the feasible region.
b.Identify the optimal solution point on your graph. What are the values of X and Y at the optimal solution?
c.What is the optimal value of the objective function?
(Essay)
4.9/5  (33)
(33)
Which of the following special cases does not require reformulation of the problem in order to obtain a solution?
(Multiple Choice)
4.8/5  (33)
(33)
To find the optimal solution to a linear programming problem using the graphical method
(Multiple Choice)
4.8/5  (29)
(29)
The improvement in the value of the objective function per unit increase in a right-hand side is the
(Multiple Choice)
4.7/5  (28)
(28)
A range of optimality is applicable only if the other coefficient remains at its original value.
(True/False)
4.9/5  (42)
(42)
Which of the following is a valid objective function for a linear programming problem?
(Multiple Choice)
4.7/5  (33)
(33)
In a linear programming problem, the objective function and the constraints must be linear functions of the decision variables.
(True/False)
4.9/5  (34)
(34)
Does the following linear programming problem exhibit infeasibility, unboundedness, or alternate optimal solutions? Explain.
Min
3X + 3Y
s.t.
1X + 2Y ≤ 16
1X + 1Y ≤ 10
5X + 3Y ≤ 45
X , Y ≥ 0
(Essay)
4.8/5  (38)
(38)
No matter what value it has, each objective function line is parallel to every other objective function line in a problem.
(True/False)
4.9/5  (25)
(25)
Decision variables limit the degree to which the objective in a linear programming problem is satisfied.
(True/False)
4.8/5  (30)
(30)
All of the following statements about a redundant constraint are correct EXCEPT
(Multiple Choice)
4.9/5  (38)
(38)
An optimal solution to a linear programming problem can be found at an extreme point of the feasible region for the problem.
(True/False)
4.9/5  (38)
(38)
Showing 1 - 20 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)