Question 1

​Why are 0 - 1 variables sometimes called logical variables?

Accepted Answer

0 - 1 variables are sometimes called logical variables because they can represent two distinct states, typically true or false, yes or no, on or off, which align with the binary logic found in Boolean algebra. In this context, the number 0 usually represents the logical value "false," and the number 1 represents the logical value "true."

Boolean algebra, developed by George Boole in the mid-19th century, is a branch of algebra in which the values of the variables are the truth values true and false, usually denoted by 1 and 0 respectively. This binary system underpins the operation of digital computers and digital logic. Logical variables are fundamental in computer science and are used in programming languages, decision-making structures, and digital circuits.

In programming, logical variables are often declared as boolean data types, and they are used to control the flow of the program through conditional statements like if-else statements, loops, and for controlling switches and toggles in the program's logic.

In the context of mathematical modeling, statistics, and optimization, 0 - 1 variables are used to represent binary decisions in binary linear programming problems. For example, they can be used to indicate whether a particular option is chosen (1) or not chosen (0) in a model, which is essential for solving problems that involve making a series of yes/no decisions.

In summary, 0 - 1 variables are called logical variables because they are used to represent binary outcomes that are foundational to logical decision-making in mathematics, computer science, and digital electronics.

Question 2

In an all-integer linear program,

Accepted Answer

A)  all objective function coefficients must be integer. 
B)  all right-hand side values must be integer. 
C)  all variables must be integer. 
D)  all objective function coefficients and right-hand side values must be integer. 
A)  all objective function coefficients must be integer. 
B)  all right-hand side values must be integer. 
C)  all variables must be integer. 
D)  all objective function coefficients and right-hand side values must be integer. C

Question 3

Given the following all-integer linear program:
Max
3x1 + 2x2
s.t.
3x1 + x2 ≤ 9
x1 + 3x2 ≤ 7
−x1 + x2 ≤ 1
x1, x2 ≥ 0 and integer
​
a.
​
Solve the problem as a linear program ignoring the integer constraints. Show that the optimal solution to the linear program gives fractional values for both x1 and x2.
b.
​
What is the solution obtained by rounding fractions greater than of equal to 1/2 to the next larger number? Show that this solution is not a feasible solution.
c.
What is the solution obtained by rounding down all fractions? Is it feasible?
d.
​
​
Enumerate all points in the linear programming feasible region in which both x1 and x2 are integers, and show that the feasible solution obtained in (c) is not optimal and that in fact the optimal integer is not obtained by any form of rounding.

Accepted Answer

a. From the graph on the next page, the optimal solution to the linear program is x₁ = 2.5, x₂ = 1.5, z = 10.5.
b. By rounding the optimal solution of x₁ = 2.5, x₂ = 1.5 to x₁ = 3, x₂= 2, this point lies outside the feasible region.
c. By rounding the optimal solution down to x₁ = 2, x₂ = 1, we see that this solution indeed is an integer solution within the feasible region, and substituting in the objective function, it gives z = 8.
d. There are eight feasible integer solutions in the linear programming feasible region with z values as follows:

a. From the graph on the next page, the optimal solution to the linear program is x<sub>1</sub> = 2.5, x<sub>2</sub> = 1.5, z = 10.5. b. By rounding the optimal solution of x<sub>1</sub> = 2.5, x<sub>2</sub> = 1.5 to x<sub>1</sub> = 3, x<sub>2 </sub>= 2, this point lies outside the feasible region. c. By rounding the optimal solution down to x<sub>1</sub> = 2, x<sub>2</sub> = 1, we see that this solution indeed is an integer solution within the feasible region, and substituting in the objective function, it gives z = 8. d. There are eight feasible integer solutions in the linear programming feasible region with z values as follows: x<sub>1</sub> = 3, x<sub>2</sub> = 0 is the optimal solution. Rounding the LP solution (x<sub>1</sub> = 2.5, x<sub>2</sub> = 1.5) would not have been optimal.

x₁ = 3, x₂ = 0 is the optimal solution. Rounding the LP solution (x₁ = 2.5, x₂ = 1.5) would not have been optimal.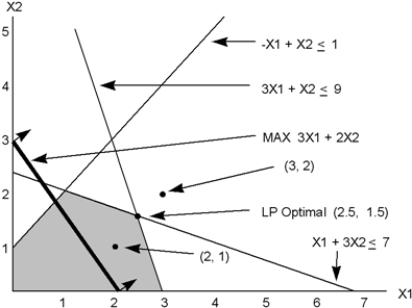

Question 4

The graph of a problem that requires x1 and x2 to be integer has a feasible region

Accepted Answer

A)  the same as its LP relaxation. 
B)  of dots. 
C)  of horizontal stripes. 
D)  of vertical stripes. 
A)  the same as its LP relaxation. 
B)  of dots. 
C)  of horizontal stripes. 
D)  of vertical stripes.

Question 5

Grush Consulting has five projects to consider. Each will require time in the next two quarters according to the table below.   ​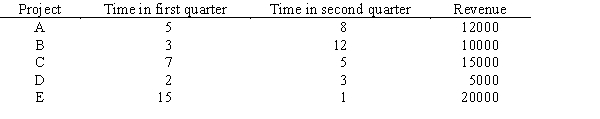
Revenue from each project is also shown. Develop a model whose solution would maximize revenue, meet the time budget of 25 in the first quarter and 20 in the second quarter, and not do both projects C and D.

Accepted Answer

Let A = 1 if project A is sele

Question 6

Which of the following is the most useful contribution of integer programming?

Accepted Answer

A)  finding whole number solutions where fractional solutions would not be appropriate 
B)  using 0-1 variables for modeling flexibility 
C)  increased ease of solution 
D)  provision for solution procedures for transportation and assignment problems 
A)  finding whole number solutions where fractional solutions would not be appropriate 
B)  using 0-1 variables for modeling flexibility 
C)  increased ease of solution 
D)  provision for solution procedures for transportation and assignment problems

Question 7

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables, rounding down will always provide a feasible integer solution.

Accepted Answer

A) True 
 B)False

Question 8

If the LP relaxation of an integer program has a feasible solution, then the integer program has a feasible solution.

Accepted Answer

A) True 
 B)False

Question 9

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

Accepted Answer

A) True 
 B)False

Question 10

Solve the following problem graphically.
Max
5X + 6Y
s.t.
17X + 8Y ≤ 136
3X + 4Y ≤ 36
X, Y ≥ 0 and integer
​
a.Graph the constraints for this problem. Indicate all feasible solutions.
b.Find the optimal solution to the LP Relaxation. Round down to find a feasible integer solution. Is this solution optimal?
c.Find the optimal solution.

Accepted Answer

a.The feasible region is those integer v

Question 11

Rounded solutions to linear programs must be evaluated for

Accepted Answer

A)  feasibility and optimality. 
B)  sensitivity and duality. 
C)  relaxation and boundedness. 
D)  each of these choices are true. 
A)  feasibility and optimality. 
B)  sensitivity and duality. 
C)  relaxation and boundedness. 
D)  each of these choices are true.

Question 12

Solve the following problem graphically.
Max
X + 2Y
s.t.
6X + 8Y ≤ 48
7X + 5Y ≥ 35
X, Y ≥ 0
Y is integer
​
a.Graph the constraints for this problem. Indicate all feasible solutions.
b.Find the optimal solution to the LP Relaxation. Round down to find a feasible integer solution. Is this solution optimal?
c.Find the optimal solution.

Accepted Answer

a.The feasible region consists of the po

Question 13

Tom's Tailoring has five idle tailors and four custom garments to make. The estimated time (in hours) it would take each tailor to make each garment is listed below. (An 'X' in the table indicates an unacceptable tailor-garment assignment.)
​​   ​
Formulate and solve an integer program for determining the tailor-garment assignments that minimize the total estimated time spent making the four garments. No tailor is to be assigned more than one garment and each garment is to be worked on by only one tailor.

Accepted Answer

Solution:
Assign wedding gown

Question 14

Kloos Industries has projected the availability of capital over each of the next three years to be $850,000, $1,000,000, and $1,200,000, respectively. It is considering four options for the disposition of the capital:
(1)
Research and development of a promising new product
(2)
Plant expansion
(3)
Modernization of its current facilities
(4)
Investment in a valuable piece of nearby real estate
​
Monies not invested in these projects in a given year will NOT be available for following year's investment in the projects. The expected benefits three years hence from each of the four projects and the yearly capital outlays of the four options are summarized in the table below in $1,000,000's.
In addition, Kloos has decided to undertake exactly two of the projects, and if plant expansion is selected, it will also modernize its current facilities.   ​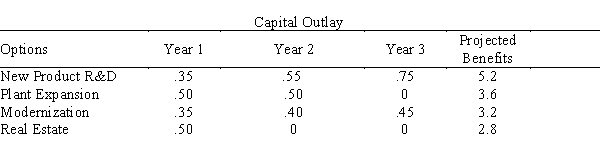
Formulate and solve this problem as a binary programming problem.

Accepted Answer

Solution: X₁ = 1, X₂ =

Question 15

In general, rounding large values of decision variables to the nearest integer value causes fewer problems than rounding small values.

Accepted Answer

A) True 
 B)False

Question 16

Sensitivity analysis for integer linear programming

Accepted Answer

A)  can be provided only by computer. 
B)  has precisely the same interpretation as that from linear programming. 
C)  does not have the same interpretation and should be disregarded. 
D)  is most useful for 0 - 1 models. 
A)  can be provided only by computer. 
B)  has precisely the same interpretation as that from linear programming. 
C)  does not have the same interpretation and should be disregarded. 
D)  is most useful for 0 - 1 models.

Question 17

If the optimal solution to the LP relaxation problem is integer, it is the optimal solution to the integer linear program.

Accepted Answer

A) True 
 B)False

Question 18

The classic assignment problem can be modeled as a 0-1 integer program.

Accepted Answer

A) True 
 B)False

Question 19

If x1 + x2 ≤ 500y1 and y1 is 0 - 1, then if y1 is 0, x1 and x2 will be 0.

Accepted Answer

A) True 
 B)False

Question 20

​Explain how integer and 0-1 variables can be used in a constraint to enable production.

Accepted Answer

Integer and 0-1 variables can be used in

Why are 0 - 1 variables sometimes called logical variables?

In an all-integer linear program,

The graph of a problem that requires x₁ and x₂ to be integer has a feasible region

Which of the following is the most useful contribution of integer programming?

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables, rounding down will always provide a feasible integer solution.

If the LP relaxation of an integer program has a feasible solution, then the integer program has a feasible solution.

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

Rounded solutions to linear programs must be evaluated for

In general, rounding large values of decision variables to the nearest integer value causes fewer problems than rounding small values.

Sensitivity analysis for integer linear programming

If the optimal solution to the LP relaxation problem is integer, it is the optimal solution to the integer linear program.

The classic assignment problem can be modeled as a 0-1 integer program.

If x₁ + x₂ ≤ 500y₁ and y₁ is 0 - 1, then if y₁ is 0, x₁ and x₂ will be 0.

Explain how integer and 0-1 variables can be used in a constraint to enable production.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Distribution and Network Models

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

Exam 7: Integer Linear Programming

​Why are 0 - 1 variables sometimes called logical variables?

In an all-integer linear program,

The graph of a problem that requires x1 and x2 to be integer has a feasible region

Which of the following is the most useful contribution of integer programming?

If a problem has only less-than-or-equal-to constraints with positive coefficients for the variables, rounding down will always provide a feasible integer solution.

If the LP relaxation of an integer program has a feasible solution, then the integer program has a feasible solution.

Dual prices cannot be used for integer programming sensitivity analysis because they are designed for linear programs.

Rounded solutions to linear programs must be evaluated for

In general, rounding large values of decision variables to the nearest integer value causes fewer problems than rounding small values.

Sensitivity analysis for integer linear programming

If the optimal solution to the LP relaxation problem is integer, it is the optimal solution to the integer linear program.

The classic assignment problem can be modeled as a 0-1 integer program.

If x1 + x2 ≤ 500y1 and y1 is 0 - 1, then if y1 is 0, x1 and x2 will be 0.

​Explain how integer and 0-1 variables can be used in a constraint to enable production.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Distribution and Network Models

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

Why are 0 - 1 variables sometimes called logical variables?

The graph of a problem that requires x₁ and x₂ to be integer has a feasible region

If x₁ + x₂ ≤ 500y₁ and y₁ is 0 - 1, then if y₁ is 0, x₁ and x₂ will be 0.

Explain how integer and 0-1 variables can be used in a constraint to enable production.