Question 1

​Define the variables and constraints necessary in the LP formulation of the transshipment problem.

Accepted Answer

The transshipment problem involves determining the optimal flow of goods from multiple sources to multiple destinations, while also allowing for intermediate transshipment points where goods can be temporarily stored and transferred. In the LP formulation of the transshipment problem, the following variables and constraints are necessary:

Variables:
1. Flow variables: These represent the amount of goods flowing from a source to a destination, or from a transshipment point to another point. These variables are typically denoted as Xij, where i represents the source or transshipment point, and j represents the destination or transshipment point.

Constraints:
1. Supply constraints: These constraints ensure that the total amount of goods leaving each source does not exceed its supply capacity.
2. Demand constraints: These constraints ensure that the total amount of goods arriving at each destination meets its demand requirements.
3. Transshipment constraints: These constraints ensure that the total amount of goods entering a transshipment point equals the total amount leaving the transshipment point, taking into account any storage or transfer capabilities at the transshipment point.
4. Non-negativity constraints: These constraints ensure that the flow variables are non-negative, as goods cannot flow in negative quantities.

By formulating the transshipment problem as an LP with these variables and constraints, it becomes possible to optimize the flow of goods while satisfying the supply, demand, and transshipment requirements.

Question 2

When a route in a transportation problem is unacceptable, the corresponding variable can be removed from the LP formulation.

Accepted Answer

A) True 
 B)False  True

Question 3

A computer manufacturing company wants to develop a monthly plan for shipping finished products from three of its manufacturing facilities to three regional warehouses. It is thinking about using a transportation LP formulation to exactly match capacities and requirements. Data on transportation costs (in dollars per unit), capacities, and requirements are given below.
​   ​ 
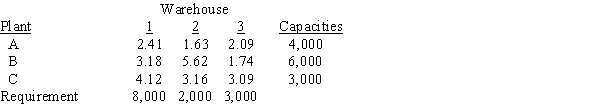
a. How many variables are involved in the LP formulation?
b. How many constraints are there in this problem?
c. What is the constraint corresponding to Plant B?
d. What is the constraint corresponding to Warehouse 3?

Accepted Answer

The problem formulation is shown below. Use it to answer the questions a - D.
X_ij = each combination of plant i and warehouse j
Min 2.41X_A1 + 1.63X_A2 + 2.09X_A3 + 3.18X_B1 + 5.62X_B2 + 1.74X_B3
+ 4.12X_C1 + 3.16X_C2 + 3.09X_C3
st X_A1 + X_A2 +X_A3 = 4,000 (capacities) X_A1 + X_B1 +X_C1 = 8,000 (requirements)X_B1 + X_B2 + X_B3 = 6,000 X_A2 + X_B2 +X_C2 = 2,000
X_C1 +X_C2 + X_C3 = 3,000 X_A3 + X_B3 +X_C3 = 3,000

a. 9 variables
b. 6 constraints
c. X_B1 + X_B2 + X_B3 = 6,000
d. X_A3 + X_B3 +X_C3 = 3,000

Question 4

​Explain what adjustments can be made to the transportation linear program when there are unacceptable routes.

Accepted Answer

When there are unacceptable routes in a

Question 5

Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.

Accepted Answer

A) True 
 B)False

Question 6

Show both the network and the linear programming formulation for this assignment problem.
​   ​

Accepted Answer

@#IMG-DLM& Let X_ij = 1 if person i is assigned to

Question 7

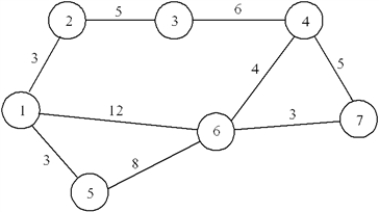
A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket.
​

Accepted Answer

Min 3X₁₂ + 3X₁₅ + 12X₁₆ + 5X₂₃ + 5X₃₂ + 6X₃₄ + 6X

Question 8

A professor has been contacted by four not-for-profit agencies that are willing to work with student consulting teams. The agencies need help with such things as budgeting, information systems, coordinating volunteers, and forecasting. Although each of the four student teams could work with any of the agencies, the professor feels that there is a difference in the amount of time it would take each group to solve each problem. The professor's estimate of the time, in days, is given in the table below. Use the computer solution to see which team works with which project.   ASSIGNMENT PROBLEM
************************
OBJECTIVE: MINIMIZATION
SUMMARY OF UNIT COST OR REVENUE DATA
*********************************************   OPTIMAL ASSIGNMENTS COST/REVENUE
************************ ***************

Accepted Answer

Team A works with the forecast

Question 9

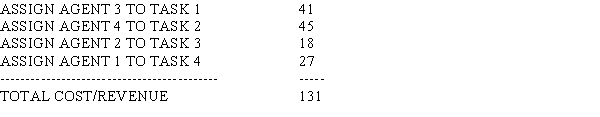
Which of the following is not a characteristic of assignment problems?​

Accepted Answer

A)  ​costs appear in the objective function only 
B)  ​the RHS of all constraints is 1 
C)  ​the value of all decision variables is either 0 or 1 
D)  ​the signs of constraints are always < 
A)  ​costs appear in the objective function only 
B)  ​the RHS of all constraints is 1 
C)  ​the value of all decision variables is either 0 or 1 
D)  ​the signs of constraints are always <

Question 10

The objective of the transportation problem is to

Accepted Answer

A)  identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost. 
B)  minimize the number of origins used to satisfy total demand at the destinations. 
C)  minimize the number of shipments necessary to satisfy total demand at the destinations. 
D)  minimize the cost of shipping products from several origins to several destinations. 
A)  identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost. 
B)  minimize the number of origins used to satisfy total demand at the destinations. 
C)  minimize the number of shipments necessary to satisfy total demand at the destinations. 
D)  minimize the cost of shipping products from several origins to several destinations.

Question 11

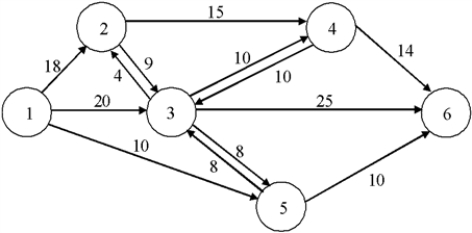
The network below shows the flows possible between pairs of six locations. Formulate an LP to find the maximal flow possible from Node 1 to Node 6.
​

Accepted Answer

The answer of The network below shows the flows possible...

Question 12

The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.

Accepted Answer

A) True 
 B)False

Question 13

The assignment problem is a special case of the

Accepted Answer

A)  transportation problem. 
B)  transshipment problem. 
C)  maximal flow problem. 
D)  shortest-route problem. 
A)  transportation problem. 
B)  transshipment problem. 
C)  maximal flow problem. 
D)  shortest-route problem.

Question 14

A transshipment problem is a generalization of the transportation problem in which certain nodes are neither supply nodes nor destination nodes.

Accepted Answer

A) True 
 B)False

Question 15

Arcs in a transshipment problem

Accepted Answer

A)  must connect every node to a transshipment node. 
B)  represent the cost of shipments. 
C)  indicate the direction of the flow. 
D)  All of the alternatives are correct. 
A)  must connect every node to a transshipment node. 
B)  represent the cost of shipments. 
C)  indicate the direction of the flow. 
D)  All of the alternatives are correct.

Question 16

The difference between the transportation and assignment problems is that

Accepted Answer

A)  total supply must equal total demand in the transportation problem 
B)  the number of origins must equal the number of destinations in the transportation problem 
C)  each supply and demand value is 1 in the assignment problem 
D)  there are many differences between the transportation and assignment problems 
A)  total supply must equal total demand in the transportation problem 
B)  the number of origins must equal the number of destinations in the transportation problem 
C)  each supply and demand value is 1 in the assignment problem 
D)  there are many differences between the transportation and assignment problems

Question 17

The assignment problem constraint x31 + x32 + x33 + x34 ≤ 2 means

Accepted Answer

A)  agent 3 can be assigned to 2 tasks. 
B)  agent 2 can be assigned to 3 tasks. 
C)  a mixture of agents 1, 2, 3, and 4 will be assigned to tasks. 
D)  there is no feasible solution. 
A)  agent 3 can be assigned to 2 tasks. 
B)  agent 2 can be assigned to 3 tasks. 
C)  a mixture of agents 1, 2, 3, and 4 will be assigned to tasks. 
D)  there is no feasible solution.

Question 18

If a transportation problem has four origins and five destinations, the LP formulation of the problem will have nine constraints.

Accepted Answer

A) True 
 B)False

Question 19

​How is the assignment linear program different from the transportation model?

Accepted Answer

The assignment linear program and the tr

Question 20

The assignment problem is a special case of the transportation problem in which all supply and demand values equal one.

Accepted Answer

A) True 
 B)False

Define the variables and constraints necessary in the LP formulation of the transshipment problem.

When a route in a transportation problem is unacceptable, the corresponding variable can be removed from the LP formulation.

Explain what adjustments can be made to the transportation linear program when there are unacceptable routes.

Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.

Show both the network and the linear programming formulation for this assignment problem.

A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket.

Which of the following is not a characteristic of assignment problems?

The objective of the transportation problem is to

The network below shows the flows possible between pairs of six locations. Formulate an LP to find the maximal flow possible from Node 1 to Node 6.

The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.

The assignment problem is a special case of the

A transshipment problem is a generalization of the transportation problem in which certain nodes are neither supply nodes nor destination nodes.

Arcs in a transshipment problem

The difference between the transportation and assignment problems is that

The assignment problem constraint x₃₁ + x₃₂ + x₃₃ + x₃₄ ≤ 2 means

If a transportation problem has four origins and five destinations, the LP formulation of the problem will have nine constraints.

How is the assignment linear program different from the transportation model?

The assignment problem is a special case of the transportation problem in which all supply and demand values equal one.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Integer Linear Programming

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

Exam 6: Distribution and Network Models

​Define the variables and constraints necessary in the LP formulation of the transshipment problem.

When a route in a transportation problem is unacceptable, the corresponding variable can be removed from the LP formulation.

​Explain what adjustments can be made to the transportation linear program when there are unacceptable routes.

Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.

Show both the network and the linear programming formulation for this assignment problem. ​ ​

A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket. ​

Which of the following is not a characteristic of assignment problems?​

The objective of the transportation problem is to

The network below shows the flows possible between pairs of six locations. Formulate an LP to find the maximal flow possible from Node 1 to Node 6. ​

The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.

The assignment problem is a special case of the

A transshipment problem is a generalization of the transportation problem in which certain nodes are neither supply nodes nor destination nodes.

Arcs in a transshipment problem

The difference between the transportation and assignment problems is that

The assignment problem constraint x31 + x32 + x33 + x34 ≤ 2 means

If a transportation problem has four origins and five destinations, the LP formulation of the problem will have nine constraints.

​How is the assignment linear program different from the transportation model?

The assignment problem is a special case of the transportation problem in which all supply and demand values equal one.

Introduction

An Introduction to Linear Programming

Linear Programming: Sensitivity Analysis and Interpretation of Solution

Linear Programming Applications in Marketing, Finance, and Operations Management

Advanced Linear Programming Applications

Integer Linear Programming

Nonlinear Optimization Models

Project Scheduling: Pertcpm

Inventory Models

Waiting Line Models

Simulation

Decision Analysis

Multicriteria Decisions

Time Series Analysis and Forecasting

Markov Processes

Linear Programming: Simplex Method

Simplex-Based Sensitivity Analysis and Duality

Solution Procedures for Transportation and Assignment Problems

Minimal Spanning Tree

Dynamic Programming

Filters

Define the variables and constraints necessary in the LP formulation of the transshipment problem.

Explain what adjustments can be made to the transportation linear program when there are unacceptable routes.

Show both the network and the linear programming formulation for this assignment problem.

A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket.

Which of the following is not a characteristic of assignment problems?

The network below shows the flows possible between pairs of six locations. Formulate an LP to find the maximal flow possible from Node 1 to Node 6.

The assignment problem constraint x₃₁ + x₃₂ + x₃₃ + x₃₄ ≤ 2 means

How is the assignment linear program different from the transportation model?