Exam 16: Markov Processes
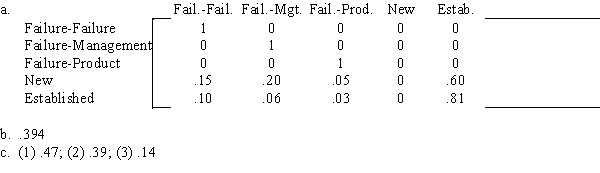
A recent study done by an economist for the Small Business Administration investigated failures of small business. Failures were either classified as due to poor financing, poor management, or a poor product. The failure rates differed for new businesses (under one year old) versus established businesses (over one year old.)
As the result of the economist's study, the following probabilities were determined. For new businesses the probability of failure due to financing was .15, due to management .20, and due to product .05. The corresponding probabilities for established businesses were .10, .06, and .03 respectively.
a.Determine a five-state Markov Chain transition matrix with states for new, established, and each of the three failure states. Write it in the form of I, O, R, and Q submatrices.
b.Determine the probability that a new business will survive during the next three years.
c.What proportion of new businesses eventually fail due to:(1) poor financing? (2) poor management? (3) poor product?
Where is a fundamental matrix, N, used? How is N computed?
A fundamental matrix, denoted as N, is used in the field of differential equations, specifically in the context of linear homogeneous systems of first-order differential equations. It is a matrix solution to a system of linear differential equations and plays a crucial role in understanding the behavior of the solutions to these systems.
In the context of a linear system of differential equations, the system can be written in matrix form as:
dx/dt = A(t) x,
where x is a vector of functions representing the system's state, A(t) is a time-dependent matrix, and t represents time.
The fundamental matrix N(t) is a square matrix whose columns are linearly independent solutions to the system. It satisfies the equation:
dN/dt = A(t) N,
with the initial condition that N(t0) is an invertible matrix, often chosen to be the identity matrix I for simplicity.
The fundamental matrix is important because once it is found, any solution to the system can be expressed as a linear combination of the columns of N. If x(t) is a solution to the system, then there exists a constant vector c such that:
x(t) = N(t) c.
The computation of the fundamental matrix N can be done in several ways, depending on the nature of the matrix A(t):
1. **Constant Coefficients:** If A(t) is a constant matrix, the fundamental matrix can be computed using the matrix exponential, N(t) = exp(A t), where exp denotes the matrix exponential function.
2. **Variation of Parameters:** For non-constant A(t), one can use the method of variation of parameters. This involves guessing a form for N(t) and then determining the unknown functions by plugging N(t) into the differential equation and solving the resulting equations.
3. **Series Solutions:** When A(t) has a specific form, such as periodicity or other properties, series solutions can be used to construct N(t) by assuming a series form for the solutions and determining the coefficients.
4. **Numerical Methods:** When an analytical solution is not feasible, numerical methods such as the Runge-Kutta method can be used to approximate N(t) by discretizing the time variable and iteratively solving the system of equations.
5. **Diagonalization or Jordan Normal Form:** If A is diagonalizable, N(t) can be computed by diagonalizing A and then taking the matrix exponential of the diagonal matrix. If A is not diagonalizable, one can use its Jordan normal form to compute the matrix exponential and hence the fundamental matrix.
The computation of the fundamental matrix is a fundamental tool in the analysis of linear systems of differential equations, as it provides a way to understand the complete solution space of the system.
Two airlines offer conveniently scheduled flights to the airport nearest your corporate headquarters. Historically, flights have been scheduled as reflected in this transition matrix. 
a.
If your last flight was on B, what is the probability your next flight will be on A?
b.
If your last flight was on B, what is the probability your second next flight will be on A?
c.
What are the steady state probabilities?
a.
If your last flight was on B, what is the probability your next flight will be on A?
b.
If your last flight was on B, what is the probability your second next flight will be on A?
c.
What are the steady state probabilities?
a..2
B..28
C.1/3, 2/3
All Markov chain transition matrices have the same number of rows as columns.
If an absorbing state exists, then the probability that a unit will ultimately move into the absorbing state is given by the steady state probability.
A city is served by three cable TV companies: Xcellent Cable, Your Cable, and Zephyr Cable. A survey of 1000 cable subscribers shows this breakdown of customers from the beginning to the end of August.
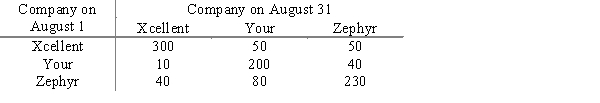
a.Construct the transition matrix.
b.What was each company's share of the market at the beginning and the end of the month?
c.If the current trend continues what will the market shares be?
a.Construct the transition matrix.
b.What was each company's share of the market at the beginning and the end of the month?
c.If the current trend continues what will the market shares be?
The sum of the probabilities in a transition matrix equals the number of rows in the matrix.
The probability of going from state 1 in period 2 to state 4 in period 3 is
If the probability of making a transition from a state is 0, then that state is called a(n)
The probability that the system is in state 2 in the 5th period is π5(2).
All entries in a row of a matrix of transition probabilities sum to 1.
When absorbing states are present, each row of the transition matrix corresponding to an absorbing state will have a single 1 and all other probabilities will be 0.
Rent-To-Keep rents household furnishings by the month. At the end of a rental month a customer can: a) rent the item for another month, b) buy the item, or c) return the item. The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks. 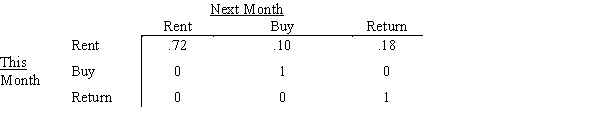 What is the probability that a customer who rented a TV this month will eventually buy it?
What is the probability that a customer who rented a TV this month will eventually buy it?
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)