SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.4276 \\ \text { R Square } & 0.1828 \\ \text { Adjusted R Square } & 0.1457 \\ \text { Standard Error } & 5.7351 \\ \text { Observations } & 47 \\ \hline \end{array}\\\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & \text { F } & { \text { Significance } F } \\ \hline \text { Regression } & 2 & 323.8284 & 161.9142 & 4.9227 & 0.0118 \\ \text { Residual } & 44 & 1447.2094 & 32.8911 & & \\ \text { Total } & 46 & 1771.0378 & & & \\ \hline \end{array}\\\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & { t \text { Stat } } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & - 72.9916 & 45.9106 & - 1.5899 & 0.1190 & - 165.5184 & 19.5352 \\ \text { Salary } & 2.7939 & 0.8974 & 3.1133 & 0.0032 & 0.9853 & 4.6025 \\ \text { Spending } & 0.3742 & 0.9782 & 0.3825 & 0.7039 & - 1.5972 & 2.3455 \\ \hline \end{array} \end{array}\] -Referring to SCENARIO 13-15, what is the p-value of the test statistic when testing whether mean teacher salary has any effect on percentage of students passing the proficiency test, considering the effect of instructional spending per pupil?

The answer of SCENARIO 13-15 The superintendent of a school district...

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.8535 \\ \text { R Square } & 0.7284 \\ \text { Adjusted R Square } & 0.6964 \\ \text { Standard Error } & 10.5630 \\ \text { Observations } & 20 \\ \hline \end{array}\\\\ \text { ANOYA }\\ \begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & \text { F } & \text { Siqnificonce F } \\ \hline \text { Regression } & 2 & 5086.5764 & 2543.2882 & 22.7941 & 0.0000 \\ \text { Residual } & 17 & 1896.8050 & 111.5768 & & \\ \text { Total } & 19 & 6983.3814 & & & \\ \hline \end{array}\\\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & { t \text { Stat } } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 1.5740 & 9.2723 & 0.1698 & 0.8672 & - 17.9888 & 21.1368 \\ \text { Age } & 1.3045 & 0.1956 & 6.6678 & 0.0000 & 0.8917 & 1.7173 \\ \text { Exper } & - 0.1478 & 0.1944 & - 0.7604 & 0.4574 & - 0.5580 & 0.2624 \\ \hline \end{array} \end{array}\] -Referring to SCENARIO 13-8, the analyst wants to use a t test to test for the significance of the coefficient of X2.The value of the test statistic is .

The answer of SCENARIO 13-8 A financial analyst wanted to examine...

SCENARIO 13-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr} \hline{\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8479 \\ \text { R Square } & 0.7189 \\ \text { Adjusted R Square } & 0.7069 \\ \text { Standard Error } & 17.5571 \\ \text { Observations } & 50\\ \hline \end{array}$ $\text { ANOVA }$ $\begin{array}{lrrrrr} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & & & 37043.3236 & 18521.6618 & 0.0000 \\ \text { Residual } & & 14487.7627 & 308.2503 & \\ \text { Total } & & 49 & 51531.0863 & & \end{array}$ $\begin{array}{lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & \text { P-value } \\ \hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\ \text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\ \text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\\ \hline \end{array}$ $\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$ -Referring to SCENARIO 13-4, one individual in the sample had an annual income of $40,000 and a family size of 1.This individual owned a home with an area of 1,000 square feet (House =10.00).What is the residual (in hundreds of square feet) for this data point?

The answer of SCENARIO 13-4 A real estate builder wishes to...

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.8535 \\ \text { R Square } & 0.7284 \\ \text { Adjusted R Square } & 0.6964 \\ \text { Standard Error } & 10.5630 \\ \text { Observations } & 20 \\ \hline \end{array}\\\\ \text { ANOYA }\\ \begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & \text { F } & \text { Siqnificonce F } \\ \hline \text { Regression } & 2 & 5086.5764 & 2543.2882 & 22.7941 & 0.0000 \\ \text { Residual } & 17 & 1896.8050 & 111.5768 & & \\ \text { Total } & 19 & 6983.3814 & & & \\ \hline \end{array}\\\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & { t \text { Stat } } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 1.5740 & 9.2723 & 0.1698 & 0.8672 & - 17.9888 & 21.1368 \\ \text { Age } & 1.3045 & 0.1956 & 6.6678 & 0.0000 & 0.8917 & 1.7173 \\ \text { Exper } & - 0.1478 & 0.1944 & - 0.7604 & 0.4574 & - 0.5580 & 0.2624 \\ \hline \end{array} \end{array}\] -Referring to SCENARIO 13-8, the value of the coefficient of multiple determination is_.

The answer of SCENARIO 13-8 A financial analyst wanted to examine...

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.8535 \\ \text { R Square } & 0.7284 \\ \text { Adjusted R Square } & 0.6964 \\ \text { Standard Error } & 10.5630 \\ \text { Observations } & 20 \\ \hline \end{array}\\\\ \text { ANOYA }\\ \begin{array} { l r c c c c } & d f & \text { SS } & \text { MS } & \text { F } & \text { Siqnificonce F } \\ \hline \text { Regression } & 2 & 5086.5764 & 2543.2882 & 22.7941 & 0.0000 \\ \text { Residual } & 17 & 1896.8050 & 111.5768 & & \\ \text { Total } & 19 & 6983.3814 & & & \\ \hline \end{array}\\\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & { t \text { Stat } } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 1.5740 & 9.2723 & 0.1698 & 0.8672 & - 17.9888 & 21.1368 \\ \text { Age } & 1.3045 & 0.1956 & 6.6678 & 0.0000 & 0.8917 & 1.7173 \\ \text { Exper } & - 0.1478 & 0.1944 & - 0.7604 & 0.4574 & - 0.5580 & 0.2624 \\ \hline \end{array} \end{array}\] -Referring to SCENARIO 13-8, _% of the variation in salary can be explained by the variation in age while holding experience constant.

The answer of SCENARIO 13-8 A financial analyst wanted to examine...

SCENARIO 13-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: $\begin{array}{lr} \hline{\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8479 \\ \text { R Square } & 0.7189 \\ \text { Adjusted R Square } & 0.7069 \\ \text { Standard Error } & 17.5571 \\ \text { Observations } & 50\\ \hline \end{array}$ $\text { ANOVA }$ $\begin{array}{lrrrrr} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & & & 37043.3236 & 18521.6618 & 0.0000 \\ \text { Residual } & & 14487.7627 & 308.2503 & \\ \text { Total } & & 49 & 51531.0863 & & \end{array}$ $\begin{array}{lrrrr} \hline & \text { Coefficients } & \text { Standard Error } &{t \text { Stat }} & \text { P-value } \\ \hline \text { Intercept } & -5.5146 & 7.2273 & -0.7630 & 0.4493 \\ \text { Income } & 0.4262 & 0.0392 & 10.8668 & 0.0000 \\ \text { Size } & 5.5437 & 1.6949 & 3.2708 & 0.0020\\ \hline \end{array}$ $\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$ -Referring to SCENARIO 13-4, what fraction of the variability in house size is explained by income and size of family?

A) 17.56% B) 70.69% C) 71.89% D) 84.79% A) 17.56% B) 70.69% C) 71.89% D) 84.79%

SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.4276 \\ \text { R Square } & 0.1828 \\ \text { Adjusted R Square } & 0.1457 \\ \text { Standard Error } & 5.7351 \\ \text { Observations } & 47 \\ \hline \end{array}\\\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & \text { F } & { \text { Significance } F } \\ \hline \text { Regression } & 2 & 323.8284 & 161.9142 & 4.9227 & 0.0118 \\ \text { Residual } & 44 & 1447.2094 & 32.8911 & & \\ \text { Total } & 46 & 1771.0378 & & & \\ \hline \end{array}\\\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \text { Standard Error } & { t \text { Stat } } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & - 72.9916 & 45.9106 & - 1.5899 & 0.1190 & - 165.5184 & 19.5352 \\ \text { Salary } & 2.7939 & 0.8974 & 3.1133 & 0.0032 & 0.9853 & 4.6025 \\ \text { Spending } & 0.3742 & 0.9782 & 0.3825 & 0.7039 & - 1.5972 & 2.3455 \\ \hline \end{array} \end{array}\] -Referring to SCENARIO 13-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

A) $H _ { 1 } : \beta _ { 0 } = \beta _ { 1 } = \beta _ { 2 } \neq 0$ B) $H _ { 1 } : \beta _ { 1 } = \beta _ { 2 } \neq 0$ C) $H _ { 1 } \text { : At least one of } \beta _ { j } \neq 0 \text { for } j = 0,1,2$ D) $H _ { 1 } \text { : At least one of } \beta _ { j } \neq 0 \text { for } j = 1,2$ A) $H _ { 1 } : \beta _ { 0 } = \beta _ { 1 } = \beta _ { 2 } \neq 0$ B) $H _ { 1 } : \beta _ { 1 } = \beta _ { 2 } \neq 0$ C) $H _ { 1 } \text { : At least one of } \beta _ { j } \neq 0 \text { for } j = 0,1,2$ D) $H _ { 1 } \text { : At least one of } \beta _ { j } \neq 0 \text { for } j = 1,2$

SCENARIO 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.5270 \\ \text { R Square } & 0.2778 \\ \text { Adjusted R Square } & 0.1928 \\ \text { Standard Error } & 40.9107 \\ \text { Observations } & 20 \\ \hline \end{array}\\ \end{array}\] $\begin{array}{lrrrrr} \text { ANOVA }\\ \hline&\text { df } & \text { SS } & \text { MS } & F & \text { Significance F }\\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\ \text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\ \text { Total } & 19 & 39395.6218 & & & \end{array}$ 13-22 Multiple Regression \[\begin{array}{l} \begin{array} { l r r r r r r } \hline & \text { Coefficients } &{ \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\ \text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\ \text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\ \hline \end{array}\\ \text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672 \end{array}\] -Referring to SCENARIO 13-6 and allowing for a 1% probability of committing a type I error,what is the decision and conclusion for the testH :$\beta$1 -$\beta$2- 0 vs.H : At least one $\beta$j$\neq$ 0, j -1, 20 1 2 1 j?

A) Do not reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs. B) Do not reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs. C) Reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs. D) Reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs. A) Do not reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs. B) Do not reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs. C) Reject H0 and conclude that the 2 independent variables taken as a group have significant linear effects on heating costs. D) Reject H0 and conclude that the 2 independent variables taken as a group do not have significant linear effects on heating costs.

SCENARIO 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. \[\begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.5270 \\ \text { R Square } & 0.2778 \\ \text { Adjusted R Square } & 0.1928 \\ \text { Standard Error } & 40.9107 \\ \text { Observations } & 20 \\ \hline \end{array}\\ \end{array}\] $\begin{array}{lrrrrr} \text { ANOVA }\\ \hline&\text { df } & \text { SS } & \text { MS } & F & \text { Significance F }\\ \hline\text { Regression } & 2 & 10943.0190 & 5471.5095 & 3.2691 & 0.0629 \\ \text { Residual } & 17 & 28452.6027 & 1673.6825 & & \\ \text { Total } & 19 & 39395.6218 & & & \end{array}$ 13-22 Multiple Regression \[\begin{array}{l} \begin{array} { l r r r r r r } \hline & \text { Coefficients } &{ \text { Standard Error } } & { \text { t Stat } } & \text { P-volue } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & 448.2925 & 90.7853 & 4.9379 & 0.0001 & 256.7522 & 639.8328 \\ \text { Temperature } & - 2.7621 & 1.2371 & - 2.2327 & 0.0393 & - 5.3721 & - 0.1520 \\ \text { Insulation } & - 15.9408 & 10.0638 & - 1.5840 & 0.1316 & - 37.1736 & 5.2919 \\ \hline \end{array}\\ \text { Also } \operatorname { SSR } \left( X _ { 1 } \mid X _ { 2 } \right) = 8343.3572 \text { and } \operatorname { SSR } \left( X _ { 2 } \mid X _ { 1 } \right) = 4199.2672 \end{array}\] -Referring to SCENARIO 13-6, what is the 95% confidence interval for the expected change in heating costs as a result of a 1 degree Fahrenheit change in the daily minimum outside temperature?

A) [256.7522, 639.8328] B) [204.7854, 497.1733] C) [-5.3721, -0.1520] D) [-37.1736, 5.2919] A) [256.7522, 639.8328] B) [204.7854, 497.1733] C) [-5.3721, -0.1520] D) [-37.1736, 5.2919]

SCENARIO 13-7 The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units and total SAT scores of each.She takes a sample of 6 students and generates the following Microsoft Excel output: SUMMARY OUTPUT Regression Statistics $\begin{array} { l l } \text { Multiple R } & 0.916 \\ \text { R Square } & 0.839 \\ \text { Adjusted R Square } & 0.732 \\ \text { Standard Error } & 0.24685 \\ \text { Observations } & 6 \end{array}$ ANOVA $\begin{array} { l r c c r c } & d f & \text { SS } & \text { MS } & F & \text { Signif } F \\ \text { Regression } & 2 & 0.95219 & 0.47610 & 7.813 & 0.0646 \\ \text { Residual } & 3 & 0.18281 & 0.06094 & & \\ \text { Total } & 5 & 1.13500 & & & \end{array}$ $\begin{array} { l c r c c } & \text { Coeff } & \text { StdError } & t \text { Stat } & P \text {-value } \\ \text { Intercept } & 4.593897 & 1.13374542 & 4.052 & 0.0271 \\ \text { Units } & - 0.247270 & 0.06268485 & - 3.945 & 0.0290 \\ \text { Total SAT } & 0.001443 & 0.00101241 & 1.425 & 0.2494 \end{array}$ -Referring to SCENARIO 13-7, the department head wants to test H0: $\beta$1 = $\beta$2 = 0 .The value of the F-test statistic is _.

The answer of SCENARIO 13-7 The department head of the accounting...

SCENARIO 13-13 An econometrician is interested in evaluating the relationship of demand for building materials to mortgage rates in Los Angeles and San Francisco.He believes that the appropriate model is \[Y = 10 + 5 X _ { 1 } + 8 X _ { 2 }\] where \[\begin{array} { l } X _ { 1 } = \text { mortgage rate in } \% \\ X _ { 2 } = 1 \text { if SF, } 0 \text { if LA } \\ Y = \text { demand in } \$ 100 \text { per capita } \end{array}\] -Referring to SCENARIO 13-13, the fitted model for predicting demand in Los Angeles is_.

A) 10 + 5X1 B) 10 + 13X1 C) 15 + 8X2 D) 18 + 5X2 A) 10 + 5X1 B) 10 + 13X1 C) 15 + 8X2 D) 18 + 5X2

Exam 13: Multiple Regression

SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA df SS MS F Significance F Regression 2 323.8284 161.9142 4.9227 0.0118 Residual 44 1447.2094 32.8911 Total 46 1771.0378 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to SCENARIO 13-15, what is the p-value of the test statistic when testing whether mean teacher salary has any effect on percentage of students passing the proficiency test, considering the effect of instructional spending per pupil?

(Short Answer)

4.9/5

(34)

Question 101

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 ANOYA df SS MS F Siqnificonce F Regression 2 5086.5764 2543.2882 22.7941 0.0000 Residual 17 1896.8050 111.5768 Total 19 6983.3814 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 -Referring to SCENARIO 13-8, the analyst wants to use a t test to test for the significance of the coefficient of X2.The value of the test statistic is .

(Short Answer)

4.8/5

(40)

Question 102

SCENARIO 13-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: Regression Statistics Multiple R 0.8479 R Square 0.7189 Adjusted R Square 0.7069 Standard Error 17.5571 Observations 50 $\text { ANOVA }$ df SS MS F Significance F Regression 37043.3236 18521.6618 0.0000 Residual 14487.7627 308.2503 Total 49 51531.0863 Coefficients Standard Error t Stat P-value Intercept -5.5146 7.2273 -0.7630 0.4493 Income 0.4262 0.0392 10.8668 0.0000 Size 5.5437 1.6949 3.2708 0.0020 $\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$ -Referring to SCENARIO 13-4, one individual in the sample had an annual income of $40,000 and a family size of 1.This individual owned a home with an area of 1,000 square feet (House =10.00).What is the residual (in hundreds of square feet) for this data point?

(Short Answer)

4.8/5

(34)

Question 103

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 ANOYA df SS MS F Siqnificonce F Regression 2 5086.5764 2543.2882 22.7941 0.0000 Residual 17 1896.8050 111.5768 Total 19 6983.3814 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 -Referring to SCENARIO 13-8, the value of the coefficient of multiple determination is_.

(Short Answer)

4.9/5

(34)

Question 104

SCENARIO 13-8 A financial analyst wanted to examine the relationship between salary (in $1,000) and 2 variables: age (X1 = Age) and experience in the field (X2 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: Regression Statistics Multiple R 0.8535 R Square 0.7284 Adjusted R Square 0.6964 Standard Error 10.5630 Observations 20 ANOYA df SS MS F Siqnificonce F Regression 2 5086.5764 2543.2882 22.7941 0.0000 Residual 17 1896.8050 111.5768 Total 19 6983.3814 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 1.5740 9.2723 0.1698 0.8672 -17.9888 21.1368 Age 1.3045 0.1956 6.6678 0.0000 0.8917 1.7173 Exper -0.1478 0.1944 -0.7604 0.4574 -0.5580 0.2624 -Referring to SCENARIO 13-8, _% of the variation in salary can be explained by the variation in age while holding experience constant.

(Short Answer)

4.7/5

(39)

Question 105

SCENARIO 13-4 A real estate builder wishes to determine how house size (House) is influenced by family income (Income) and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: Regression Statistics Multiple R 0.8479 R Square 0.7189 Adjusted R Square 0.7069 Standard Error 17.5571 Observations 50 $\text { ANOVA }$ df SS MS F Significance F Regression 37043.3236 18521.6618 0.0000 Residual 14487.7627 308.2503 Total 49 51531.0863 Coefficients Standard Error t Stat P-value Intercept -5.5146 7.2273 -0.7630 0.4493 Income 0.4262 0.0392 10.8668 0.0000 Size 5.5437 1.6949 3.2708 0.0020 $\text { Also } \operatorname{SSR}\left(X_{1} \mid X_{2}\right)=36400.6326 \text { and } \operatorname{SSR}\left(X_{2} \mid X_{1}\right)=3297.7917$ -Referring to SCENARIO 13-4, what fraction of the variability in house size is explained by income and size of family?

(Multiple Choice)

4.9/5

(35)

Question 106

The following two statements are equivalent in meaning:A.The test of significance for a specific regression coefficient in a multiple regression model is a test of significance for adding that variable into the model given the other variable is included.B.The t test for a regression coefficient is actually a test for the contribution of that independent variable.

(True/False)

4.8/5

(33)

Question 107

SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA df SS MS F Significance F Regression 2 323.8284 161.9142 4.9227 0.0118 Residual 44 1447.2094 32.8911 Total 46 1771.0378 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to SCENARIO 13-15, which of the following is the correct alternative hypothesis to determine whether there is a significant relationship between percentage of students passing the proficiency test and the entire set of explanatory variables?

(Multiple Choice)

4.8/5

(26)

Question 108

SCENARIO 13-3 An economist is interested to see how consumption for an economy (in $ billions) is influenced by gross domestic product ($ billions) and aggregate price (consumer price index).The Microsoft Excel output of this regression is partially reproduced below. 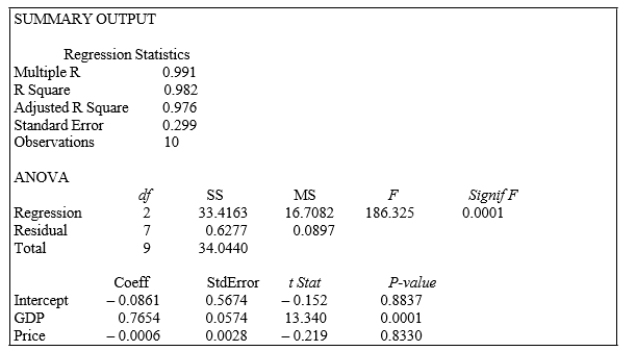-Referring to SCENARIO 13-3, to test whether aggregate price index has a negative impact on consumption, the p-value is ?

(Multiple Choice)

4.8/5

(32)

Question 109

SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA df SS MS F Significance F Regression 2 323.8284 161.9142 4.9227 0.0118 Residual 44 1447.2094 32.8911 Total 46 1771.0378 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to SCENARIO 13-15, there is sufficient evidence that the percentageof students passing the proficiency test depends on both of the explanatory variables at a 5% level of significance.

(True/False)

4.9/5

(33)

Question 110

SCENARIO 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. Regression Statistics Multiple R 0.5270 R Square 0.2778 Adjusted R Square 0.1928 Standard Error 40.9107 Observations 20 ANOVA df SS MS F Significance F Regression 2 10943.0190 5471.5095 3.2691 0.0629 Residual 17 28452.6027 1673.6825 Total 19 39395.6218 13-22 Multiple Regression Coefficients Standard Error t Stat P-volue Lower 95\% Upper 95\% Intercept 448.2925 90.7853 4.9379 0.0001 256.7522 639.8328 Temperature -2.7621 1.2371 -2.2327 0.0393 -5.3721 -0.1520 Insulation -15.9408 10.0638 -1.5840 0.1316 -37.1736 5.2919 Also SSR \mid =8343.3572 and SSR \mid =4199.2672 -Referring to SCENARIO 13-6 and allowing for a 1% probability of committing a type I error,what is the decision and conclusion for the testH : $\beta$ 1 - $\beta$ 2- 0 vs.H : At least one $\beta$ j $\neq$ 0, j -1, 20 1 2 1 j?

(Multiple Choice)

4.9/5

(43)

Question 111

SCENARIO 13-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit ( X1 ) and the amount of insulation in inches ( X 2 ).Given below is EXCEL output of the regression model. Regression Statistics Multiple R 0.5270 R Square 0.2778 Adjusted R Square 0.1928 Standard Error 40.9107 Observations 20 ANOVA df SS MS F Significance F Regression 2 10943.0190 5471.5095 3.2691 0.0629 Residual 17 28452.6027 1673.6825 Total 19 39395.6218 13-22 Multiple Regression Coefficients Standard Error t Stat P-volue Lower 95\% Upper 95\% Intercept 448.2925 90.7853 4.9379 0.0001 256.7522 639.8328 Temperature -2.7621 1.2371 -2.2327 0.0393 -5.3721 -0.1520 Insulation -15.9408 10.0638 -1.5840 0.1316 -37.1736 5.2919 Also SSR \mid =8343.3572 and SSR \mid =4199.2672 -Referring to SCENARIO 13-6, what is the 95% confidence interval for the expected change in heating costs as a result of a 1 degree Fahrenheit change in the daily minimum outside temperature?

(Multiple Choice)

4.8/5

(25)

Question 112

SCENARIO 13-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no). The results of the regression analysis are given below: Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40 ANOVA df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to SCENARIO 13-17, there is sufficient evidence that the number of weeks a worker is unemployed due to a layoff depends on all of the explanatory variables at a10% level of significance.

(True/False)

4.8/5

(33)

Question 113

SCENARIO 13-2 A professor of industrial relations believes that an individual's wage rate at a factory (Y) depends on his performance rating (X1) and the number of economics courses the employee successfully completed in college (X2).The professor randomly selects 6 workers and collects the following information: Employee Y(\ ) 1 10 3 0 2 12 1 5 3 15 8 1 4 17 5 8 5 20 7 12 6 25 10 9 -Referring to SCENARIO 13-2, for these data, what is the value for the regression constant, b0?

(Multiple Choice)

4.8/5

(33)

Question 114

SCENARIO 13-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no). The results of the regression analysis are given below: Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40 ANOVA df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to SCENARIO 13-17, we can conclude definitively that, holding constant the effect of the other independent variable, age has an impact on the mean number of weeks a worker is unemployed due to a layoff at a 10% level of significance if all we have is the information of the 95% confidence interval estimate for the effect of a one year increase in age on the mean number of weeks a worker is unemployed due to a layoff.

(True/False)

4.9/5

(32)

Question 115

SCENARIO 13-7 The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units and total SAT scores of each.She takes a sample of 6 students and generates the following Microsoft Excel output: SUMMARY OUTPUT Regression Statistics Multiple R 0.916 R Square 0.839 Adjusted R Square 0.732 Standard Error 0.24685 Observations 6 ANOVA df SS MS F Signif F Regression 2 0.95219 0.47610 7.813 0.0646 Residual 3 0.18281 0.06094 Total 5 1.13500 Coeff StdError t Stat P -value Intercept 4.593897 1.13374542 4.052 0.0271 Units -0.247270 0.06268485 -3.945 0.0290 Total SAT 0.001443 0.00101241 1.425 0.2494 -Referring to SCENARIO 13-7, the department head wants to test H0: $\beta$ 1 = $\beta$ 2 = 0 .The value of the F-test statistic is _.

(Short Answer)

4.8/5

(28)

Question 116

SCENARIO 13-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth- grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending) of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, X1 = Salaries and X 2 = Spending: Regression Statistics Multiple R 0.4276 R Square 0.1828 Adjusted R Square 0.1457 Standard Error 5.7351 Observations 47 ANOVA df SS MS F Significance F Regression 2 323.8284 161.9142 4.9227 0.0118 Residual 44 1447.2094 32.8911 Total 46 1771.0378 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept -72.9916 45.9106 -1.5899 0.1190 -165.5184 19.5352 Salary 2.7939 0.8974 3.1133 0.0032 0.9853 4.6025 Spending 0.3742 0.9782 0.3825 0.7039 -1.5972 2.3455 -Referring to SCENARIO 13-15, you can conclude definitively that mean teacher salary individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of instructional spending per pupil, at a 1% level of significance based solely on but not actually computing the 99% confidence interval estimate for $\beta$ 1 .

(True/False)

4.8/5

(41)

Question 117

Which of the following is NOT used to determine observations that have influential effect on the fitted model?

(Multiple Choice)

4.9/5

(23)

Question 118

SCENARIO 13-13 An econometrician is interested in evaluating the relationship of demand for building materials to mortgage rates in Los Angeles and San Francisco.He believes that the appropriate model is $Y = 10 + 5 X _ { 1 } + 8 X _ { 2 }$ where = mortgage rate in \% =1 if SF, 0 if LA Y= demand in \ 100 per capita -Referring to SCENARIO 13-13, the fitted model for predicting demand in Los Angeles is_.

(Multiple Choice)

4.8/5

(41)

Question 119

SCENARIO 13-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy) and the independent variables are the age of the worker (Age) and a dummy variable for management position (Manager: 1 = yes, 0 = no). The results of the regression analysis are given below: Regression Statistics Multiple R 0.6391 R Square 0.4085 Adjusted R Square 0.3765 Standard Error 18.8929 Observations 40 ANOVA df SS MS F Significance F Regression 2 9119.0897 4559.5448 12.7740 0.0000 Residual 37 13206.8103 356.9408 Total 39 22325.9 Coefficients Standard Error t Stat P -value Intercept -0.2143 11.5796 -0.0185 0.9853 Age 1.4448 0.3160 4.5717 0.0000 Manager -22.5761 11.3488 -1.9893 0.0541 -Referring to SCENARIO 13-17, you can conclude that, holding constant the effect of the other independent variable, age has no impact on the mean number of weeks a worker is unemployed due to a layoff at a 5% level of significance if we use only the information of the 95% confidence interval estimate for the effect of a one year increase in age on the mean number of weeks a worker is unemployed due to a layoff.

(True/False)

4.9/5

(28)

Question 120

Which of the following is NOT used to determine observations that have influential effect on the fitted model?

Defining and Collecting Data

Organizing and Visualizing Variables

Numerical Descriptive Measures

Basic Probability

Discrete Probability Distributions

The Normal Distribution

Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Two-Sample Tests

Chi-Square Tests

Simple Linear Regression

Business Analytics

Filters