Exam 1: Introduction and Mathematical Concepts
Exam 1: Introduction and Mathematical Concepts67 Questions
Exam 2: Kinematics in One Dimension103 Questions
Exam 3: Kinematics in Two Dimensions68 Questions
Exam 4: Forces and Newtons Laws of Motion103 Questions
Exam 5: Dynamics of Uniform Circular Motion59 Questions
Exam 6: Work and Energy78 Questions
Exam 7: Impulse and Momentum65 Questions
Exam 8: Rotational Kinematics55 Questions
Exam 9: Rotational Dynamics57 Questions
Exam 10: Simple Harmonic Motion and Elasticity63 Questions
Exam 11: Fluids65 Questions
Exam 12: Temperature and Heat66 Questions
Exam 13: The Transfer of Heat42 Questions
Exam 14: The Ideal Gas Law and Kinetic Theory55 Questions
Exam 15: Thermodynamics79 Questions
Exam 16: Waves and Sound67 Questions
Exam 17: The Principle of Linear Superposition and Interference Phenomena51 Questions
Exam 18: Electric Forces and Electric Fields61 Questions
Exam 19: Electric Potential Energy and the Electric Potential70 Questions
Exam 20: Electric Circuits99 Questions
Exam 21: Magnetic Forces and Magnetic Fields66 Questions
Exam 22: Electromagnetic Induction71 Questions
Exam 23: Alternating Current Circuits84 Questions
Exam 24: Electromagnetic Waves66 Questions
Exam 25: The Reflection of Light: Mirrors42 Questions
Exam 26: The Refraction of Light: Lenses and Optical Instruments102 Questions
Exam 27: Interference and the Wave Nature of Light57 Questions
Exam 28: Special Relativity62 Questions
Exam 29: Particles and Waves54 Questions
Exam 30: The Nature of the Atom73 Questions
Exam 31: Nuclear Physics and Radioactivity33 Questions
Exam 32: Ionizing Radiation, Nuclear Energy, and Elementary Particles43 Questions
Select questions type
Which one of the following answers would give the correct number of significant figures when the following masses are added together: 3.6 kg, 113 kg, and 4.19 kg?
(Multiple Choice)
4.8/5  (35)
(35)
During the execution of a play, a football player carries the ball for a distance of 33 m in the direction 58° north of east.To determine the number of meters gained on the play, find the northward component of the ball's displacement.
(Multiple Choice)
4.9/5  (37)
(37)
A sailboat leaves a harbor and sails 1.8 km in the direction 65° south of east, where the captain stops for lunch.A short time later, the boat sails 1.1 km in the direction 15° north of east.What is the magnitude of the resultant displacement from the harbor?
(Multiple Choice)
4.8/5  (42)
(42)
Complete the following statement: Today, the standard meter is defined in terms of
(Multiple Choice)
4.9/5  (36)
(36)
A vector 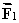 has a magnitude of 40.0 units and points 35.0° above the positive x axis.A second vector
has a magnitude of 40.0 units and points 35.0° above the positive x axis.A second vector 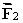 has a magnitude of 65.0 units and points in the negative x direction.Use the component method of vector addition to find the magnitude and direction, relative to the positive x axis, of the resultant
has a magnitude of 65.0 units and points in the negative x direction.Use the component method of vector addition to find the magnitude and direction, relative to the positive x axis, of the resultant 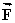 =
= 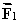 +
+ 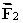 .
.
(Multiple Choice)
4.8/5  (35)
(35)
Two vectors 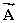 and
and 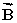 , are added together to form the vector
, are added together to form the vector 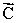 =
= 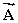 +
+ 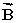 .The relationship between the magnitudes of these vectors is given by: Cx = A cos 30° + B and Cy = -A sin 30°.Which statement best describes the orientation of these vectors?
.The relationship between the magnitudes of these vectors is given by: Cx = A cos 30° + B and Cy = -A sin 30°.Which statement best describes the orientation of these vectors?
(Multiple Choice)
4.7/5  (35)
(35)
A pole is held vertically by attaching wires at a height of 13.4 m above the ground.The other end of each wire is anchored in the ground at a distance of 9.54 m from the base of the pole.The pole makes a right angle with the ground.What is the length of each wire?
(Multiple Choice)
4.8/5  (33)
(33)
The distance d that a certain particle moves may be calculated from the expression d = at + bt2 where a and b are constants; and t is the elapsed time.What must the dimensions of the quantities a and b be, respectively?
(Multiple Choice)
4.7/5  (38)
(38)
Justine and her friends exit the physics classroom and walk 0.70 km to their math class.While walking, Justine's average step length is 58 cm.Approximately, how many steps does she take in walking between these two classes?
(Multiple Choice)
4.9/5  (35)
(35)
Four members of the Main Street Bicycle Club meet at a certain intersection on Main Street.The members then start from the same location, but travel in different directions.A short time later, displacement vectors for the four members are: 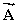 = 2.0 km, east;
= 2.0 km, east; 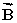 = 5.2 km, north;
= 5.2 km, north; 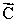 = 4.9 km, west;
= 4.9 km, west; 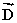 = 3.0 km, south What is the resultant displacement
= 3.0 km, south What is the resultant displacement 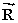 of the members of the bicycle club:
of the members of the bicycle club: 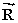 =
= 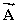 +
+ 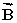 +
+ 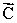 +
+ 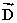 ?
?
(Multiple Choice)
4.8/5  (29)
(29)
Which one of the following choices is equivalent to 44.5 mm?
(Multiple Choice)
4.9/5  (40)
(40)
Which one of the following statements is true concerning scalar quantities?
(Multiple Choice)
4.8/5  (28)
(28)
Three vectors 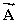 ,
, 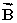 , and
, and 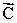 add together to yield zero:
add together to yield zero:  +
+ 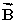 +
+ 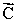 = 0.The vectors
= 0.The vectors 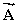 and
and 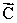 point in opposite directions and their magnitudes are related by the expression: A = 2C.Which one of the following conclusions is correct?
point in opposite directions and their magnitudes are related by the expression: A = 2C.Which one of the following conclusions is correct?
(Multiple Choice)
4.8/5  (27)
(27)
What is the minimum number of vectors with unequal magnitudes whose vector sum can be zero?
(Multiple Choice)
4.8/5  (40)
(40)
Use the component method of vector addition to find the components of the resultant of the four displacements shown in the figure.The magnitudes of the displacements are: A = 2.25 cm, B = 6.35 cm, C = 5.47 cm, and D = 4.19 cm. 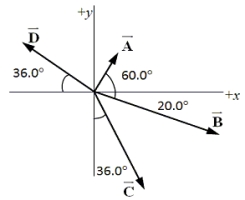 x component y component
x component y component
(Multiple Choice)
4.9/5  (32)
(32)
Two displacement vectors of magnitudes 21 cm and 79 cm are added.Which one of the following is the only possible choice for the magnitude of the resultant?
(Multiple Choice)
4.9/5  (45)
(45)
In a diving competition, a woman dives from a platform that is ten meters above the surface of the water.What is the height, expressed in feet, of the platform?
(Multiple Choice)
4.9/5  (34)
(34)
Showing 41 - 60 of 67
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)