Exam 10: Regression With Panel Data

'Empirical studies of economic growth are flawed because many of the truly important underlying determinants, such as culture and institutions, are very hard to measure.' Discuss this statement paying particular attention to simple cross-section data and panel data models.Use equations whenever possible to underscore your argument.

The "before and after" specification, binary variable specification, and "entity- demeaned" specification produce identical OLS estimates

You learned in intermediate macroeconomics that certain macroeconomic growth models predict conditional convergence or a catch up effect in per capita GDP between the countries of the world.That is, countries which are further behind initially in per-capita GDP will grow faster than the leader.You gather data from the Penn World Tables to test this theory. (a)By limiting your sample to 24 OECD countries, you hope to have a more homogeneous set of countries in your sample, i.e., countries that are not too different with respect to their institutions.To simplify matters, you decide to only test for unconditional convergence.In that case, the laggards catch up even without taking into account differences in some of the driving variables.Your scatter plot and regression for the time period 1975-1989 are as follows: 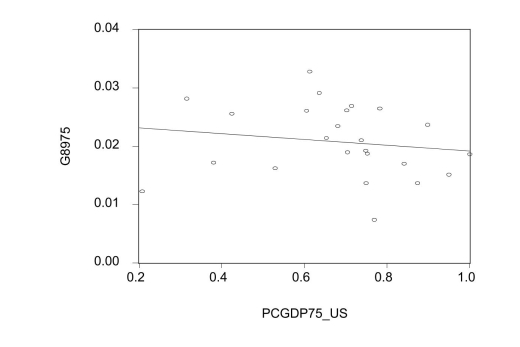= 0.024-0.005PCGDP7US;=0.025,SER=0.006 (0.06)(0.008) where $\widehat { g 8975 }$ is the average annual growth rate of per capita GDP from 1975-1989, and PCGDP75_US is per capita GDP relative to the United States in 1975. Numbers in parenthesis are heteroskedasticity-robust standard errors. Interpret the results.Is there indication of unconditional convergence? What critical value did you use?

One of the following is a regression example for which Entity and Time Fixed Effects could be used: a study of the effect of

Consider the special panel case where T=2 . If some of the omitted variables, which you hope to capture in the changes analysis, in fact change over time, then the estimator on the included change regressor

(Requires Matrix Algebra)Consider the time and entity fixed effect model with a single explanatory variable $Y _ { i t } = \beta _ { 0 } + \beta _ { 1 } X _ { i t } + \gamma _ { 2 } D 2 _ { i } + \ldots + \gamma _ { n } D n _ { i } + \delta _ { 2 } B 2 _ { t } + \ldots + \delta _ { T } B T _ { t } + u _ { i t }$ For the case of $n = 4$ and $T = 3$ , write this model in the form $\boldsymbol { Y } = \boldsymbol { X } \boldsymbol { \beta } + \boldsymbol { U }$ , where, in general, $\boldsymbol { Y } = \left( \begin{array} { l } Y _ { 1 } \\Y _ { 2 } \\\vdots \\Y _ { n }\end{array} \right) , \boldsymbol { U } = \left( \begin{array} { l } u _ { 1 } \\u _ { 2 } \\\vdots \\u _ { n }\end{array} \right) , \boldsymbol { X } = \left( \begin{array} { c c c c } 1 & X _ { 11 } & \cdots & X _ { k 1 } \\1 & X _ { 12 } & \cdots & X _ { k 2 } \\\vdots & \vdots & \ddots & \vdots \\1 & X _ { 1 n } & \cdots & X _ { k n }\end{array} \right) = \left( \begin{array} { l } \boldsymbol { X } _ { 1 } ^ { \prime } \\\boldsymbol { X } _ { 2 } ^ { \prime } \\\vdots \\\boldsymbol { X } _ { n } ^ { \prime }\end{array} \right) \text {, and } \boldsymbol { \beta } = \left( \begin{array} { l } \beta _ { 0 } \\\beta _ { 1 } \\\vdots \\\beta _ { k }\end{array} \right)$ How would the $\boldsymbol { X }$ matrix change if you added two binary variables, $D 1$ and $B 1$ ? Demonstrate that in this case the columns of the $\boldsymbol { X }$ matrix are not independent. Finally show that elimination of one of the two variables is not sufficient to get rid of the multicollinearity problem. In terms of the OLS estimator, $\hat { \boldsymbol { \beta } } = \left( \boldsymbol { X } ^ { \prime } \boldsymbol { X } \right) ^ { - 1 } \boldsymbol { X } ^ { \prime } \boldsymbol { Y }$ , why does perfect multicollinearity create a problem?

Consider the regression example from your textbook, which estimates the effect of beer taxes on fatality rates across the 48 contiguous U.S.states.If beer taxes were set Nationally by the federal government rather than by the states, then

With Panel Data, regression software typically uses an "entity-demeaned" algorithm because

(Requires Appendix material) When the fifth assumption in the Fixed Effects regression $\left( \operatorname { cov } \left( u _ { i t } , u _ { i s } \mid X _ { i i } , X _ { i s } \right) = 0 \text { for } t \neq s \right)$ is violated, then

When you add state fixed effects to a simple regression model for U.S.states over a certain time period, and the regression R2 increases significantly, then it is safe to assume That

Time Fixed Effects regression are useful in dealing with omitted variables

The main advantage of using panel data over cross sectional data is that it

Panel data is also called

cov $\left( u _ { i t } , u _ { i s } \mid X _ { i t } , X _ { i s } \right) = 0 \text { for } t \neq s$ means that

A pattern in the coefficients of the time fixed effects binary variables may reveal the following in a study of the determinants of state unemployment rates using panel data:

A study attempts to investigate the role of the various determinants of regional Canadian unemployment rates in order to get a better picture of Canadian aggregate unemployment rate behavior.The annual data (1967-1991)is for five regions (Atlantic region, Quebec, Ontario, Prairies, and British Columbia), and four age-gender groups (female and male, adult and young).Focusing on young females, the authors find significant effects for the following variables: the regional relative minimum wage rate (minimum wages divided by average hourly earnings), the regional share of youth in the labor force, the regional share of adult females in the labor force, United States activity shocks (deviations of United States GDP from trend), an indicator of the degree of monetary tightness in Canada, regional union density, and a regional index of unemployment insurance generosity.Explain why the authors only used region fixed effects.How would their specification have to change if they also employed time fixed effects?

Your textbook suggests an "entity-demeaned" procedure to avoid having to specify a potentially large number of binary variables.While it is somewhat tedious to specify a binary variable for each entity, this can still be handled relatively easily in the case of the 48 contiguous states.Give a few examples where it might be close to impossible to implement specifying such large number of entity binary variables.The idea of the "entity-demeaned" procedure was introduced as a computationally convenient and simplifying procedure.Since there are also time fixed effects, why is there no discussion of using a "time-demeaned" procedure? Using the following equation $Y _ { i t } = \beta _ { 0 } + \beta _ { 1 } X _ { i t } + \beta _ { 3 } S _ { t } + u _ { i t } ,$ $\text { Show how } \beta _ { 1 } \text { can be estimated by the OLS regression using "time-demeaned" variables. }$

Give at least three examples from macroeconomics and five from microeconomics that involve specified equations in a panel data analysis framework.Indicate in each case what the role of the entity and time fixed effects in terms of omitted variables might be.

In the Fixed Effects regression model, you should exclude one of the binary variables for the entities when an intercept is present in the equation

A study, published in 1993, used U.S.state panel data to investigate the relationship between minimum wages and employment of teenagers.The sample period was 1977 to 1989 for all 50 states.The author estimated a model of the following type: $\ln \left( E _ { i t } \right) = \beta _ { 0 } + \beta _ { 1 } \ln \left( M _ { i t } / W _ { i t } \right) + \gamma _ { 2 } D 2 _ { i } + \ldots + \gamma _ { n } D 50 _ { i } + \delta _ { 2 } B 2 _ { t } + \ldots + \delta _ { \mathrm { T } } B 13 _ { \mathrm { t } } + u _ { i t }$ where E is the employment to population ratio of teenagers, M is the nominal minimum wage, and W is average hourly earnings in manufacturing.In addition, other explanatory variables, such as the adult unemployment rate, the teenage population share, and the teenage enrollment rate in school, were included. (a)Name some of the factors that might be picked up by time and state fixed effects.