Exam 7: Arithmetic Sequence: Common Difference and First n Terms
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Find the first term and the common ratio for the geometric sequence. Round approximations to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (31)
(31)
Find the first term and the common ratio for the geometric sequence. Round approximations to the nearest hundredth.
-
(Multiple Choice)
4.8/5  (38)
(38)
Identify the equation as a parabola, circle, ellipse, or hyperbola.
-
(Multiple Choice)
4.8/5  (32)
(32)
Find the probability.
-Two 6-sided dice are rolled. What is the probability the sum of the two numbers on the die will be 5?
(Multiple Choice)
4.9/5  (38)
(38)
Provide an appropriate response.
-The sum of an infinite geometric series exists if:
(Multiple Choice)
4.9/5  (44)
(44)
100 employees of a company are asked how they get to work and whether they work full time or part time. The figure below shows the results. If one of the 100 employees is randomly selected, find the probability that the
Person does not commute by public transportation. 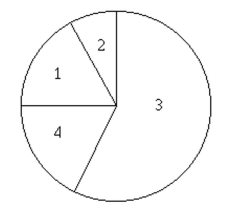 1. Public transportation: 8 full time, 8 part time
2. Bicycle: 5 full time, 3 part time
3. Drive alone: 28 full time, 33 part time
4. Car pool: 9 full time, 6 part time
1. Public transportation: 8 full time, 8 part time
2. Bicycle: 5 full time, 3 part time
3. Drive alone: 28 full time, 33 part time
4. Car pool: 9 full time, 6 part time
(Multiple Choice)
4.8/5  (39)
(39)
Write the first n terms of the given arithmetic sequence (the value of n is indicated in the question).
-The first term is 20, and the common difference is 7;
(Multiple Choice)
4.8/5  (29)
(29)
How many ways can a president, vice-president, secretary, and treasurer be chosen from a club with 10 members? Assume that no member can hold more than one office.
(Multiple Choice)
4.9/5  (29)
(29)
Decide whether the given sequence is finite or infinite.
-
(Multiple Choice)
4.9/5  (30)
(30)
Write an equation for the hyperbola.
- -intercepts , foci at
(Multiple Choice)
4.7/5  (31)
(31)
A man earned $3000 the first year he worked. If he received a raise of $600 at the end of each year, what was his salary during the 15th year?
(Multiple Choice)
4.8/5  (36)
(36)
Use the summation properties to evaluate the series. The following rules may be needed:
-
(Multiple Choice)
4.9/5  (34)
(34)
Find the eccentricity of the conic section shown in the graph.
-
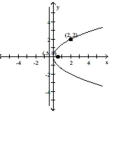
(Multiple Choice)
4.8/5  (45)
(45)
It can be shown that is true for any real number (not just positive integer values) and any real number , where . Use this series to approximate the given number to the nearest thousandth.
-
(Multiple Choice)
4.9/5  (29)
(29)
Suppose that certain bacteria can double their size and divide every 30 minutes. Write a recursive sequence that describes this growth where each value of represents a 30 -minute interval. Let represent the initial number of bacteria present.
(Multiple Choice)
4.9/5  (28)
(28)
List the elements in the sample space of the experiment.
-A box contains 10 red cards numbered 1 through 10. List the sample space of picking one card from the box.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 261 - 280 of 570
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)