Exam 7: Arithmetic Sequence: Common Difference and First n Terms
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Write an equation for the parabola with vertex at the origin.
-Through , opening downward
(Multiple Choice)
4.7/5  (42)
(42)
List the elements in the sample space of the experiment.
-A box contains 3 blue cards numbered 1 through 3, and 4 green cards numbered 1 through 4. List the sample space of picking a blue card followed by a green card.
(Multiple Choice)
4.8/5  (33)
(33)
Explain the differences between an ellipse and a hyperbola. Both definitions emphasize distance, but how is
distance used differently in these two definitions?
(Essay)
4.9/5  (34)
(34)
Suppose there are 6 roads connecting town A to town B and 4 roads connecting town B to town C. In how many ways can a person travel from A to C via B?
(Multiple Choice)
4.9/5  (33)
(33)
Determine the two equations necessary to graph the ellipse with a graphing calculator.
-
(Multiple Choice)
4.8/5  (41)
(41)
Use the summation properties to evaluate the series. The following rules may be needed:
-
(Multiple Choice)
4.7/5  (33)
(33)
Write an equation for the parabola with vertex at the origin.
-Focus
(Multiple Choice)
4.8/5  (39)
(39)
Graph the function corresponding to the sequence defined. Use the graph to decide whether the sequence converges or
diverges.
-
(Multiple Choice)
4.9/5  (34)
(34)
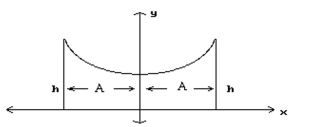
The roof of a building is in the shape of the hyperbola , where and are in meters. Refer to the figure and determine the height, , of the outside walls.
(Multiple Choice)
4.8/5  (32)
(32)
Find the first term and the common ratio for the geometric sequence. Round approximations to the nearest hundredth.
-
(Multiple Choice)
4.9/5  (33)
(33)
Showing 121 - 140 of 570
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)