Exam 7: Arithmetic Sequence: Common Difference and First n Terms
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
A sequence of yearly payments of $5000 is invested at an interest rate of 1.5%, compounded annually. What is the total amount of the annuity after 10 years?
(Multiple Choice)
4.9/5  (34)
(34)
Find the first term and the common difference for the arithmetic sequence. Round approximations to the nearest
hundredth.
-
(Multiple Choice)
4.8/5  (33)
(33)
To graph on a graphics calculator, we must consider the union of the graphs of the two functions, and . Using the graph of , explain (a) how the solution set of can be determined graphically and (b) how it relates to the domain of the hyperbola.
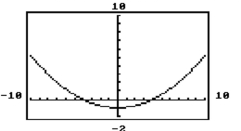
(Essay)
4.8/5  (32)
(32)
Find the sum of the first n terms of the following arithmetic sequence.
-
(Multiple Choice)
4.8/5  (35)
(35)
Martin saves $5 on the first day of a 40-day period, $10 on the second day, and so on. For the next 40 days, he increases the amount saved by $10 each day (instead of $5 each day). How much will he have saved after 80
Days?
(Multiple Choice)
4.8/5  (42)
(42)
Write an equation for the parabola with vertex at the origin.
-Through (8, 8), symmetric with respect to the y-axis
(Multiple Choice)
4.9/5  (43)
(43)
Write an equation for the hyperbola.
-vertices at ; foci at
(Multiple Choice)
4.9/5  (40)
(40)
Find the common ratio r for the given infinite geometric sequence.
-
(Multiple Choice)
4.7/5  (29)
(29)
The beginning population of a small town was 12,000 people. Due to decline in industrial growth the population has since been decreasing at a rate of 3% every year. What was the population of this town 10 years
Later?
(Multiple Choice)
4.7/5  (28)
(28)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (31)
(31)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.7/5  (36)
(36)
In how many ways can a group of 8 students be selected from 9 students?
(Multiple Choice)
4.8/5  (33)
(33)
How many different three-number "combinations" are possible on a combination lock having 25 numbers on its dial without repeating a number?
(Multiple Choice)
4.7/5  (38)
(38)
Write an equation for the ellipse.
- -intercepts -intercepts
(Multiple Choice)
4.9/5  (28)
(28)
100 employees of a company are asked how they get to work and whether they work full time or part time. The figure below shows the results. If one of the 100 employees is randomly selected, find the probability that the
Person does not work full time. 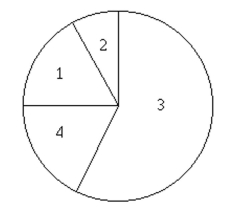 1. Public transportation: 6 full time, 7 part time
2. Bicycle: 5 full time, 5 part time
3. Drive alone: 34 full time, 28 part time
4. Car pool: 6 full time, 9 part time
1. Public transportation: 6 full time, 7 part time
2. Bicycle: 5 full time, 5 part time
3. Drive alone: 34 full time, 28 part time
4. Car pool: 6 full time, 9 part time
(Multiple Choice)
4.8/5  (44)
(44)
A lottery game has balls numbered 1 through 21. What is the probability of selecting an even numbered ball or a 11?
(Multiple Choice)
4.8/5  (38)
(38)
Showing 201 - 220 of 570
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)