Exam 7: Arithmetic Sequence: Common Difference and First n Terms
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.8/5  (32)
(32)
Graph the function corresponding to the sequence defined. Use the graph to decide whether the sequence converges or
diverges.
-
(Multiple Choice)
5.0/5  (38)
(38)
The roof of a building is in the shape of the hyperbola , where and are in meters. Refer to the figu: and determine the height of the outside walls.
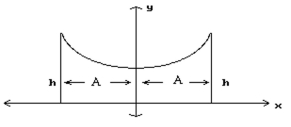
(Multiple Choice)
4.8/5  (28)
(28)
Identify the equation as a parabola, circle, ellipse, or hyperbola.
-
(Multiple Choice)
4.9/5  (36)
(36)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.9/5  (33)
(33)
Evaluate the sum using the given information.
- =-2,=-4,=2,=0, and \Delta=0.6;()=-4 \Delta
(Multiple Choice)
4.9/5  (38)
(38)
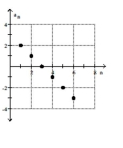
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
(Multiple Choice)
4.9/5  (37)
(37)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.8/5  (43)
(43)
If the vertex of the graph of a quadratic function lies in quadrant IV and the graph is concave up, how many x-intercepts does the graph have?
(Multiple Choice)
4.8/5  (35)
(35)
Match the equation of the parabola with the appropriate description.
-
(Multiple Choice)
4.8/5  (42)
(42)
A town has a population of 10,000 people and is increasing by 10% every year. What will the population be at the end of 5 years?
(Multiple Choice)
4.8/5  (41)
(41)
Showing 101 - 120 of 570
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)