Exam 7: Arithmetic Sequence: Common Difference and First n Terms
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Provide an appropriate response.
-Consider the selections of seven apples from a barrel of 75 apples. Is this a combination, a permutation, or neither?
(Multiple Choice)
5.0/5  (31)
(31)
Evaluate the sum. Round to two decimal places, if necessary.
-
(Multiple Choice)
4.8/5  (38)
(38)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.8/5  (37)
(37)
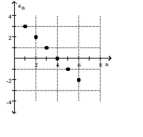
Find a formula for the nth term of the arithmetic sequence shown in the graph.
-
(Multiple Choice)
4.9/5  (26)
(26)
A student is told to work any 6 out of 10 questions on an exam. In how many different ways can he complete the exam? (The correctness of his answers has no bearing.)
(Multiple Choice)
4.9/5  (33)
(33)
Find the common difference for the arithmetic sequence.
-5, 6, 7, 8, . . .
(Multiple Choice)
4.8/5  (29)
(29)
Suppose that a family has 5 children and that the probability of having a girl is . What is the probability of having at least three boys?
(Multiple Choice)
4.8/5  (25)
(25)
Match the equation of the ellipse with the appropriate description.
-
(Multiple Choice)
4.7/5  (30)
(30)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.8/5  (33)
(33)
The series of sketches below starts with an equilateral triangle having sides of length 1 (one). In the following
steps, equilateral triangles are constructed by joining the midpoints of the sides of the preceding triangle.
Develop a formula for the length of the sides of the new triangle. 
(Short Answer)
4.9/5  (29)
(29)
In how many ways can the letters in the word PAYMENT be arranged if the letters are taken 6 at a time?
(Multiple Choice)
4.9/5  (29)
(29)
Find the common difference for the arithmetic sequence.
-8, 13, 18, 23, . . .
(Multiple Choice)
4.8/5  (30)
(30)
Use mathematical induction to prove that the statement is true for every positive integer n.
-
(Essay)
4.9/5  (34)
(34)
Evaluate the sum using the given information.
- =1,=3,=-5,=4, and \Deltax=-0.3;f(x)= f \Deltax (Round to the nearest tenth, if necessary.)
(Multiple Choice)
4.7/5  (28)
(28)
Identify the type of conic section.
-Identify the type of conic section consisting of the set of all points in the plane for which the distance from the point (0, 18) is twice the distance from the line y
(Multiple Choice)
4.9/5  (47)
(47)
When a satellite is near Earth, its orbital trajectory may trace out a hyperbola, a parabola, or an ellipse. The type of trajectory depends on the satellite's velocity in meters per second. It will be hyperbolic if , parabolic if , and elliptical if , where is a constant and is the distance in meters from the satellite to the center of Earth. Solve the problem.
-If a satellite is scheduled to leave Earth's gravitational influence, its velocity must be increased so that its trajectory changes from elliptical to hyperbolic. Determine the minimum increase in velocity necessary for a
Satellite traveling at a velocity of 5696 meters per second to escape Earth's gravitational influence when
(Multiple Choice)
4.7/5  (28)
(28)
Showing 221 - 240 of 570
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)