Question 1

$\text { A } \chi ^ { 2 } \text {-curve starts at zero and extends indefinitely to the right. }$

Accepted Answer

A) True 
 B)False

Question 2

$\mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$-curve with $\mathrm { df } = ( 11,13 )$ is equal to $1 / \mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$-curve with $\mathrm { df } = ( 13,11 )$.

Accepted Answer

A) True 
 B)False

Question 3

A sample standard deviation and sample size are given. Use the one-standard-deviation xS1U1P12S1S1P0-test to conduct the requiredhypothesis test.
-$\mathrm { s } = 13.1 , \mathrm { n } = 22$
$\mathrm { H } _ { 0 } : \sigma = 16.1 , \mathrm { H } _ { \mathrm { a } } : \sigma < 16.1 , \alpha = 0.01$

Accepted Answer

A) Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 8.897$. Do not reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 8.897$. Reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $X ^ { 2 } = 13.903$. Critical value $= 38.932$. Reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 38.932$. Do not reject $\mathrm { H } _ { 0 }$. 
A) Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 8.897$. Do not reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 8.897$. Reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $X ^ { 2 } = 13.903$. Critical value $= 38.932$. Reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $\mathrm { X } ^ { 2 } = 13.903$. Critical value $= 38.932$. Do not reject $\mathrm { H } _ { 0 }$.

Question 4

Perform the required hypothesis test for two population standard deviations. Assume that independent samples havebeen randomly selected from the two populations and that the variable under consideration is normally distributed onboth populations. Use the critical-value approach.
-A random sample of 16 women resulted in blood pressure levels with a standard deviation of 21.7 mm Hg. A random sample of 17 men resulted in blood pressure levels with a standard deviation of 19 mm Hg. Do the data provide sufficient evidence to conclude that there is more variation among blood pressure levels for women than among blood pressure levels for men? Use a 0.025 significance level .

Accepted Answer

@#LAT-DLM&  
Test statistic: @#LAT-DLM&. Critical value @#LAT-DLM&. Do

Question 5

$$\text { Use the chi-square table to find the required } \chi ^ { 2 } \text {-value(s). }$$
-For a $\chi ^ { 2 }$-curve with $\mathrm { df } = 21$, determine $\chi _ { 0.05 } ^ { 2 }$.

Accepted Answer

A) $41.401$ 
B)  $32.671$ 
C)  $11.591$ 
D)  $8.034$ 
A) $41.401$ 
B)  $32.671$ 
C)  $11.591$ 
D)  $8.034$

Question 6

A sample standard deviation and sample size are given. Use the one-standard-deviation $\chi ^ { 2 }$-interval procedure to obtain the specified confidence interval.
-s = 4, n = 11 , 95% confidence interval

Accepted Answer

A) 2.956 to 6.373 
B) 2.795 to 7.02 
C) 0.618 to 3.896 
D) 2.795 to 3.51 
A) 2.956 to 6.373 
B) 2.795 to 7.02 
C) 0.618 to 3.896 
D) 2.795 to 3.51

Question 7

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s).
-An F-curve has df = (15, 10). Find the F-value having area 0.05 to its left.

Accepted Answer

A) 2.54 
B) 0.394 
C) 0.351 
D) 2.85 
A) 2.54 
B) 0.394 
C) 0.351 
D) 2.85

Question 8

Decide whether applying one-standard-deviation chi-square procedures to the given data appears reasonable. Explainyour answer.
-Lifetimes (in hours)for a random sample of 12 batteries are as follows: $\begin{array} { l l l l l l } 57 & 59 & 61 & 64 & 72 & 76 \end{array}$ $\begin{array} { l l l l l l } 80 & 86 & 93 & 95 & 100 & 102 \end{array}$

Accepted Answer

A normal probability plot of the data is

Question 9

Perform the required hypothesis test for two population standard deviations. Assume that independent samples havebeen randomly selected from the two populations and that the variable under consideration is normally distributed onboth populations. Use the critical-value approach.
-A researcher is interested in comparing the amount of variation in women's scores on a certain test with the amount of variation in men's scores on the same test. Random samples of 11 men and 13 women yielded the following scores: $\begin{array} { l l }  \text { Men: } & 72,60,52,87,66,74,95,50,81,70,72 \ \text { Women: } & 70,78,62,96,75,68,41,74,80,47,73,94,65 \end{array}$  Do the data provide sufficient evidence to conclude that there is less variation in men's scores than in women's scores? Perform an F-test at the 5% significance level. (Note: $\left. \mathrm { s } _ { 1 } = 13.754 \text { and } \mathrm { s } _ { 2 } = 15.588 \right)$

Accepted Answer

@#LAT-DLM& 
Test statistic: @#LAT-DLM& Critical value: @#LAT-DLM& Do n

Question 10

$\mathrm { F } _ { 0.95 }$ for an $\mathrm { F }$-curve with $\mathrm { df } = ( 25,26 )$ is equal to $\mathrm { F } _ { 0.05 }$ for an $\mathrm { F }$-curve with $d f = ( 26,25 )$.

Accepted Answer

A) True 
 B)False

Question 11

A sample standard deviation and sample size are given. Use the one-standard-deviation $x ^ { 2 }$ -test to conduct the requiredhypothesis test.
-$\mathrm { s } = 4 , \mathrm { n } = 29$
$\mathrm { H } _ { 0 } : \sigma = 5.2 , \mathrm { H } _ { \mathrm { a } } : \sigma < 5.2 , \alpha = 0.025$

Accepted Answer

A) Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 44.461$. Reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $X ^ { 2 } = 21.182$. Critical value $= 44.461$. Do not reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 15.308$. Do not reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 15.308$. Reject $\mathrm { H } _ { 0 }$. 
A) Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 44.461$. Reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $X ^ { 2 } = 21.182$. Critical value $= 44.461$. Do not reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 15.308$. Do not reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $X ^ { 2 } = 16.568$. Critical value $= 15.308$. Reject $\mathrm { H } _ { 0 }$.

Question 12

Suppose that you are performing a $\chi ^ { 2 }$-test for a population standard deviation. Which of the following statements regarding the distribution of the test statistic is true?

Accepted Answer

A) If the null hypothesis is true, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n }$. 
B)  If the null hypothesis is true, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n } - 1$. 
C)  If the null hypothesis is false, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n }$. 
D)  If the null hypothesis is false, the test statistic has a chi-square distribution with $d f = n - 1$. 
A) If the null hypothesis is true, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n }$. 
B)  If the null hypothesis is true, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n } - 1$. 
C)  If the null hypothesis is false, the test statistic has a chi-square distribution with $\mathrm { df } = \mathrm { n }$. 
D)  If the null hypothesis is false, the test statistic has a chi-square distribution with $d f = n - 1$.

Question 13

The sample standard deviations and sample sizes are given for independent simple random samples from twopopulations. Use the two-standard-deviations F-test to conduct the required hypothesis test.
-$\mathrm { s } _ { 1 } = 20.9 , \mathrm { n } _ { 1 } = 16 , \mathrm {~s} _ { 2 } = 22.2 , \mathrm { n } _ { 2 } = 13$; two-tailed test, $\alpha = 0.05$

Accepted Answer

A) Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.338,3.18$. Do not reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.403,2.62$. Reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.338,3.18$. Reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.314,3.18$. Do not reject $\mathrm { H } _ { 0 }$. 
A) Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.338,3.18$. Do not reject $\mathrm { H } _ { 0 }$. 
B)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.403,2.62$. Reject $\mathrm { H } _ { 0 }$. 
C)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.338,3.18$. Reject $\mathrm { H } _ { 0 }$. 
D)  Test statistic: $\mathrm { F } = 0.89$. Critical values $= 0.314,3.18$. Do not reject $\mathrm { H } _ { 0 }$.

Question 14

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s).
-An F-curve has df = (24, 3). Find the F-value having area 0.005 to its right.

Accepted Answer

A) 42.62 
B) 0.181 
C) 5.52 
D) 8.64 
A) 42.62 
B) 0.181 
C) 5.52 
D) 8.64

Question 15

Decide whether applying one-standard-deviation chi-square procedures to the given data appears reasonable. Explainyour answer.
-A machine that fills soda bottles is supposed to fill them to a mean volume of 16.2 fluid ounces. A random sample of 20 filled bottles produced the following volumes in fluid ounces:  $\begin{array} { l l l l l l l l l l }  16.3 & 15.9 & 16.7 & 15.3 & 17.1 & 16.4 & 3.9 & 15.9 & 16.2 & 3.4 \ 16.4 & 8.2 & 15.5 & 16.5 & 16.0 & 16.3 & 15.8 & 16.7 & 16.5 & 15.5 \end{array}$

Accepted Answer

A histogram of the data is given below.

Question 16

Perform the required hypothesis test for two population standard deviations. Assume that independent samples havebeen randomly selected from the two populations and that the variable under consideration is normally distributed onboth populations. Use the critical-value approach.
-A researcher obtained independent random samples of men from two different towns. She recorded the weights of the men. The results are summarized below: $$\begin{array} { l l }  \frac { \text { Town } \mathrm { A } } { \mathrm { n } _ { 1 } = 61 } & \frac { \text { Town } \mathrm { B } } { \mathrm { n } _ { 2 } = 31 } \ \overline { \mathrm { x } } _ { 1 } = 165.1 \mathrm { lb } & \overline { \mathrm { x } } _ { 2 } = 159.5 \mathrm { lb } \ \mathrm { s } = 26.4 \mathrm { lb } & \mathrm { s } = 25.6 \mathrm { lb } \end{array}$$ Do the data provide sufficient evidence to conclude that there is more variation in weights of men from town A than in weights of men from town B? Perform an F-test at the 1% significance level.

Accepted Answer

@#LAT-DLM&  
Test statistic: @#LAT-DLM&. Critical value @#LAT-DLM&. Do

Question 17

The sample standard deviations and sample sizes are given for independent simple random samples from twopopulations. Use the two-standard-deviations F-interval procedure to obtain the specified confidence interval. Round tothe nearest hundredth.
-$\mathrm { s } _ { 1 } = 38.7 , \mathrm { n } _ { 1 } = 6 , \mathrm {~s} _ { 2 } = 84.6 , \mathrm { n } _ { 2 } = 16 ; 90 \%$ confidence interval

Accepted Answer

A) $0.27$ to $4.7$ 
B)  $0.27$ to $1.28$ 
C)  $0.46$ to $2.19$ 
D)  $0.27$ to $0.98$ 
A) $0.27$ to $4.7$ 
B)  $0.27$ to $1.28$ 
C)  $0.46$ to $2.19$ 
D)  $0.27$ to $0.98$

Question 18

The sample standard deviations and sample sizes are given for independent simple random samples from twopopulations. Use the two-standard-deviations F-interval procedure to obtain the specified confidence interval. Round tothe nearest hundredth.
-$\mathrm { s } _ { 1 } = 12.08 , \mathrm { n } _ { 1 } = 25 , \mathrm {~s} _ { 2 } = 11.05 , \mathrm { n } _ { 2 } = 21 ; 80 \%$ confidence interval

Accepted Answer

A) $0.91$ to $1.09$ 
B)  $0.69$ to $0.82$ 
C)  $0.69$ to $1.44$ 
D)  $0.82$ to $1.44$ 
A) $0.91$ to $1.09$ 
B)  $0.69$ to $0.82$ 
C)  $0.69$ to $1.44$ 
D)  $0.82$ to $1.44$

Question 19

$\text {The area under a } \chi ^ { 2 } \text {-curve to the left of } \chi _ { 0.995 } ^ { 2 } \text { is } 0.005 \text {. }$

Accepted Answer

A) True 
 B)False

Question 20

Perform the required hypothesis test for two population standard deviations. Assume that independent samples havebeen randomly selected from the two populations and that the variable under consideration is normally distributed onboth populations. Use the critical-value approach.
-Test scores for random samples of students from two different schools were recorded. The summary statistics are given below. 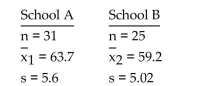  Do the data provide sufficient evidence to conclude that variation in test scores differs between students from school A and students from school B? Use a significance level of 0.10.

Accepted Answer

@#LAT-DLM&  
Test statistic: @#LAT-DLM&. Critical values @#LAT-DLM&. D

$\text { A } \chi ^ { 2 } \text {-curve starts at zero and extends indefinitely to the right. }$

$\mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 11,13 )$ is equal to $1 / \mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 13,11 )$ .

A sample standard deviation and sample size are given. Use the one-standard-deviation x²-test to conduct the requiredhypothesis test. - $\mathrm { s } = 13.1 , \mathrm { n } = 22$ $\mathrm { H } _ { 0 } : \sigma = 16.1 , \mathrm { H } _ { \mathrm { a } } : \sigma < 16.1 , \alpha = 0.01$

$\text { Use the chi-square table to find the required } \chi ^ { 2 } \text {-value(s). }$ -For a $\chi ^ { 2 }$ -curve with $\mathrm { df } = 21$ , determine $\chi _ { 0.05 } ^ { 2 }$ .

A sample standard deviation and sample size are given. Use the one-standard-deviation $\chi ^ { 2 }$ -interval procedure to obtain the specified confidence interval. -s = 4, n = 11 , 95% confidence interval

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s). -An F-curve has df = (15, 10). Find the F-value having area 0.05 to its left.

Decide whether applying one-standard-deviation chi-square procedures to the given data appears reasonable. Explainyour answer. -Lifetimes (in hours)for a random sample of 12 batteries are as follows: 57 59 61 64 72 76 80 86 93 95 100 102

$\mathrm { F } _ { 0.95 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 25,26 )$ is equal to $\mathrm { F } _ { 0.05 }$ for an $\mathrm { F }$ -curve with $d f = ( 26,25 )$ .

A sample standard deviation and sample size are given. Use the one-standard-deviation $x ^ { 2 }$ -test to conduct the requiredhypothesis test. - $\mathrm { s } = 4 , \mathrm { n } = 29$ $\mathrm { H } _ { 0 } : \sigma = 5.2 , \mathrm { H } _ { \mathrm { a } } : \sigma < 5.2 , \alpha = 0.025$

Suppose that you are performing a $\chi ^ { 2 }$ -test for a population standard deviation. Which of the following statements regarding the distribution of the test statistic is true?

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s). -An F-curve has df = (24, 3). Find the F-value having area 0.005 to its right.

$\text {The area under a } \chi ^ { 2 } \text {-curve to the left of } \chi _ { 0.995 } ^ { 2 } \text { is } 0.005 \text {. }$

The Nature of Statistics

Organizing Data

Descriptive Measures

Probability Concepts

Discrete Random Variables

The Normal Distribution

The Sampling Distribution of the Sample Mean

Confidence Intervals for One Population Mean

Hypothesis Tests for One Population Mean

Inferences for Two Population Means

Inferences for Population Proportions

Chi-Square Procedures

Descriptive Methods in Regression and Correlation

Inferential Methods in Regression and Correlation

Analysis of Variance Anova

Filters

Exam 11: Inferences for Population Standard Deviations

A χ2-curve starts at zero and extends indefinitely to the right. \text { A } \chi ^ { 2 } \text {-curve starts at zero and extends indefinitely to the right. } A χ2-curve starts at zero and extends indefinitely to the right.

F0.01\mathrm { F } _ { 0.01 }F0.01​ for an F\mathrm { F }F -curve with df=(11,13)\mathrm { df } = ( 11,13 )df=(11,13) is equal to 1/F0.011 / \mathrm { F } _ { 0.01 }1/F0.01​ for an F\mathrm { F }F -curve with df=(13,11)\mathrm { df } = ( 13,11 )df=(13,11) .

A sample standard deviation and sample size are given. Use the one-standard-deviation χ2\chi ^ { 2 }χ2 -interval procedure to obtain the specified confidence interval. -s = 4, n = 11 , 95% confidence interval

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s). -An F-curve has df = (15, 10). Find the F-value having area 0.05 to its left.

Decide whether applying one-standard-deviation chi-square procedures to the given data appears reasonable. Explainyour answer. -Lifetimes (in hours)for a random sample of 12 batteries are as follows: 57 59 61 64 72 76 80 86 93 95 100 102

F0.95\mathrm { F } _ { 0.95 }F0.95​ for an F\mathrm { F }F -curve with df=(25,26)\mathrm { df } = ( 25,26 )df=(25,26) is equal to F0.05\mathrm { F } _ { 0.05 }F0.05​ for an F\mathrm { F }F -curve with df=(26,25)d f = ( 26,25 )df=(26,25) .

Suppose that you are performing a χ2\chi ^ { 2 }χ2 -test for a population standard deviation. Which of the following statements regarding the distribution of the test statistic is true?

Use the F-table and the reciprocal property of F-curves, if necessary, to find the required F-value(s). -An F-curve has df = (24, 3). Find the F-value having area 0.005 to its right.

The area under a χ2-curve to the left of χ0.9952 is 0.005. \text {The area under a } \chi ^ { 2 } \text {-curve to the left of } \chi _ { 0.995 } ^ { 2 } \text { is } 0.005 \text {. }The area under a χ2-curve to the left of χ0.9952​ is 0.005.

The Nature of Statistics

Organizing Data

Descriptive Measures

Probability Concepts

Discrete Random Variables

The Normal Distribution

The Sampling Distribution of the Sample Mean

Confidence Intervals for One Population Mean

Hypothesis Tests for One Population Mean

Inferences for Two Population Means

Inferences for Population Proportions

Chi-Square Procedures

Descriptive Methods in Regression and Correlation

Inferential Methods in Regression and Correlation

Analysis of Variance Anova

Filters

$\text { A } \chi ^ { 2 } \text {-curve starts at zero and extends indefinitely to the right. }$

$\mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 11,13 )$ is equal to $1 / \mathrm { F } _ { 0.01 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 13,11 )$ .

A sample standard deviation and sample size are given. Use the one-standard-deviation $\chi ^ { 2 }$ -interval procedure to obtain the specified confidence interval. -s = 4, n = 11 , 95% confidence interval

$\mathrm { F } _ { 0.95 }$ for an $\mathrm { F }$ -curve with $\mathrm { df } = ( 25,26 )$ is equal to $\mathrm { F } _ { 0.05 }$ for an $\mathrm { F }$ -curve with $d f = ( 26,25 )$ .

Suppose that you are performing a $\chi ^ { 2 }$ -test for a population standard deviation. Which of the following statements regarding the distribution of the test statistic is true?

$\text {The area under a } \chi ^ { 2 } \text {-curve to the left of } \chi _ { 0.995 } ^ { 2 } \text { is } 0.005 \text {. }$