Exam 13: Chi-Square Procedures
Exam 1: The Nature of Statistics88 Questions
Exam 2: Organizing Data169 Questions
Exam 3: Descriptive Measures195 Questions
Exam 4: Probability Concepts133 Questions
Exam 5: Discrete Random Variables163 Questions
Exam 6: The Normal Distribution144 Questions
Exam 7: The Sampling Distribution of the Sample Mean76 Questions
Exam 8: Confidence Intervals for One Population Mean84 Questions
Exam 9: Hypothesis Tests for One Population Mean58 Questions
Exam 10: Inferences for Two Population Means103 Questions
Exam 11: Inferences for Population Standard Deviations101 Questions
Exam 12: Inferences for Population Proportions104 Questions
Exam 13: Chi-Square Procedures74 Questions
Exam 14: Descriptive Methods in Regression and Correlation55 Questions
Exam 15: Inferential Methods in Regression and Correlation41 Questions
Exam 16: Analysis of Variance Anova71 Questions
Select questions type
Use the contingency table to solve the problem.
-The following contingency table shows the popular votes cast in the 1984 presidential election cross classified by region and political party. Data are in thousands, rounded to the nearest thousand. 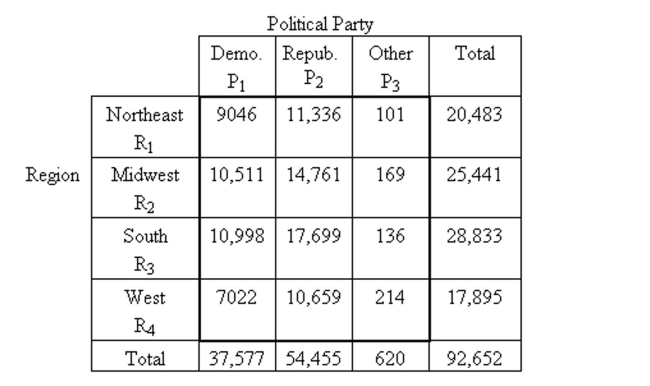 What percentage of the people voted Democrat and were in the West?
What percentage of the people voted Democrat and were in the West?
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
D
The table below shows a distribution and the observed frequencies of the values of a variable from a simple random sample of a population. Perform a chi-square goodness-of-fit test, at the specified significance level, to decide whether the distribution of the variable differs from the given distribution. 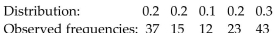 Observed frequencies: 3 Significance level
Observed frequencies: 3 Significance level
Free
(Essay)
4.8/5  (40)
(40)
Correct Answer:
-value.
-For a -curve with 27 degrees of freedom, find the -value having area to its right.
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
B
When performing a chi-square goodness-of-fit test, why do large values of the test statistic suggest that the variable does not have the distribution stated in the null hypothesis? Refer to the formula for the test statistic in your explanation.
(Essay)
4.7/5  (38)
(38)
Perform a chi-square independence test using the critical value approach, provided the conditions for using the test aremet. Be sure to state the hypotheses and the significance level, to obtain the expected frequencies, to obtain the criticalvalue, to compute the value of the test statistic, and to state your conclusion.
-The Book Industry Study Group, Inc., performs sample surveys to obtain information on characteristics of book readers. A book reader is defined to be one who read one or more books in the six months prior to the survey; a non-book reader is defined to be one who read newspapers or magazines but no books in the six months prior to the survey; a nonreader is defined to be one who did not read a book, newspaper, or magazine in the six months prior to the survey. The following data were obtained from a random sample of 1429 persons 16 years old and over. 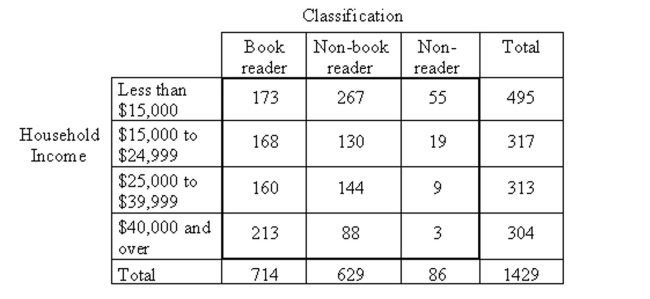 At the 1% significance level, do the data provide sufficient evidence to conclude that an association exists between "household income" and "reader classification"?
At the 1% significance level, do the data provide sufficient evidence to conclude that an association exists between "household income" and "reader classification"?
(Essay)
4.8/5  (29)
(29)
Perform a chi-square independence test using the critical value approach, provided the conditions for using the test aremet. Be sure to state the hypotheses and the significance level, to obtain the expected frequencies, to obtain the criticalvalue, to compute the value of the test statistic, and to state your conclusion.
-A researcher performed a study to determine whether an association exists between sex and blood type. He obtained the following sample data. 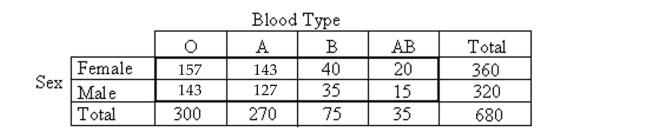 At the 5% significance level, do the data provide sufficient evidence to conclude that an association exists between sex and blood type?
At the 5% significance level, do the data provide sufficient evidence to conclude that an association exists between sex and blood type?
(Essay)
4.7/5  (40)
(40)
Perform a chi-square homogeneity test, provided the conditions for the test are met. Use the P-value approach.
-An independent simple random sample of 400 men and 400 women was asked whether they planned to attend a concert in the next month. The results are listed below, showing the concert attendance status by gender. At the 5% significance level, test the claim that a difference exists in the distribution of concert attendance status among men and women. Men Women Plan to attend concert 230 255 Don't plan to attend concert 170 145
(Essay)
4.7/5  (41)
(41)
The table below shows a distribution and the observed frequencies of the values of a variable from a simple random sample of a population. Perform a chi-square goodness-of-fit test, at the specified significance level, to decide whether the distribution of the variable differs from the given distribution.
Distribution: 0.25 0.15 0.15 0.15 0.3 Observed frequencies: 28 13 14 17 28 Significance level = 0.01
(Essay)
4.8/5  (39)
(39)
Use the contingency table to solve the problem.
-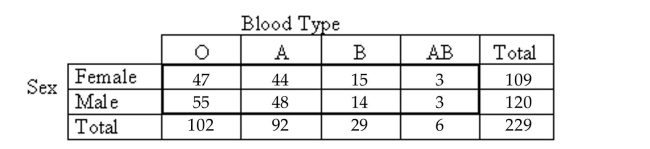 The contingency table above shows the blood types of a sample of people cross classified by sex. What percentage of those people with blood type A are women?
The contingency table above shows the blood types of a sample of people cross classified by sex. What percentage of those people with blood type A are women?
(Multiple Choice)
4.8/5  (35)
(35)
Perform the indicated goodness-of-fit test. Be sure to state the hypotheses and the significance level, to obtain the criticalvalue, to compute the value of the test statistic, and to state your conclusion.
-A firm that manufactures engines for racing boats gathers data from all of its plants. The table below gives the distribution of the life span of the engines (in numbers of months)for the entire firm.
Months Relative Frequency Under 60 0.017 70-79 0.201 80-89 0.353 90-99 0.331 100-109 0.098
Months Number of engines Under 60 22 70-79 131 80-89 46 90-99 154 100-109 95
At the 5% significance level, do the data provide evidence that the distribution of the life spans of the engines manufactured at the Ohio plant is different from the firm's overall distribution?
(Essay)
4.7/5  (35)
(35)
Perform the indicated goodness-of-fit test. Be sure to state the hypotheses and the significance level, to obtain the criticalvalue, to compute the value of the test statistic, and to state your conclusion.
-In 1990, workplace accidents were distributed on workdays as follows. Day Mon Tues Wed Thur Fri Percentage 25 15 15 15 30 In 1995, a random sample of 100 workplace accidents yielded the following data. Day Mon Tues Wed Thur Fri Percentage 21 13 15 16 35 Do the data provide sufficient evidence to conclude that the distribution of workplace accidents in 1995 differs from the 1990 distribution? Perform the hypothesis test at the 0.01 level of significance.
(Essay)
4.9/5  (42)
(42)
Perform a chi-square homogeneity test, provided the conditions for the test are met. Use the critical-value approach.
-At a high school debate tournament, half of the teams were asked to wear suits and ties and the rest were asked to wear jeans and t-shirts. The results of independent simple random samples are given in the table below. Test the hypothesis at the 5% significance level that the differently dressed debate teams are nonhomogeneous with respect to tournament wins/losses. Win Loss Suit 22 28 T-shirt 28 22
(Essay)
4.8/5  (35)
(35)
Perform a chi-square homogeneity test, provided the conditions for the test are met. Use the critical-value approach.
-A researcher wishes to test the effectiveness of a flu vaccination. 150 people are vaccinated, 180 people are vaccinated with a placebo, and 100 people are not vaccinated. Independent simple random samples were used and the number in each group who later caught the flu was recorded. The results are given in the table below, showing the test group and flu status. Vaccinated Placebo Control Caught the flu 8 19 21 Did not catch the flu 142 161 79 Use a 5% significance level to test the claim that there is a difference in the distribution of flu status for the three test groups.
(Essay)
4.7/5  (34)
(34)
The table below shows a distribution and the observed frequencies of the values of a variable from a simple random sample of a population. Perform a chi-square goodness-of-fit test, at the specified significance level, to decide whether the distribution of the variable differs from the given distribution. Distribution: 0.15 0.20 0.25 0.25 0.15 Observed frequencies: 12 15 16 18 19 Significance level =0.10
(Essay)
4.8/5  (41)
(41)
Perform a chi-square independence test using the P-value approach, provided the conditions for using the test are met.Be sure to state the hypotheses and the significance level, to obtain the expected frequencies, to compute the value of thetest statistic, to obtain the P-value, and to state your conclusion.
-A car insurance company performed a study to determine whether an association exists between age and the frequency of car accidents. They obtained the following sample data. 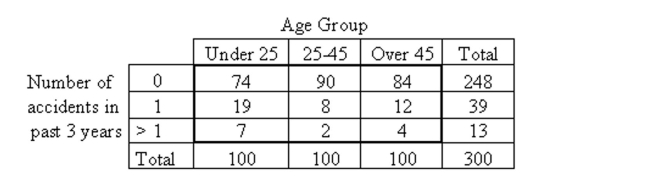 At the 5% significance level, do the data provide sufficient evidence to conclude that an association exists between age and frequency of car accidents?
At the 5% significance level, do the data provide sufficient evidence to conclude that an association exists between age and frequency of car accidents?
(Essay)
4.9/5  (38)
(38)
Suppose that you wish to perform a chi-square test of independence. The sample data is given in the contingency table below. Are the assumptions for the test met? If not, which assumption is violated? 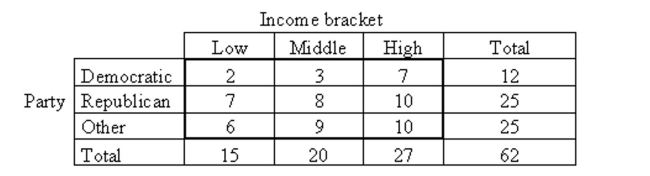
(Essay)
4.8/5  (42)
(42)
Perform the indicated goodness-of-fit test. Be sure to state the hypotheses and the significance level, to obtain the criticalvalue, to compute the value of the test statistic, and to state your conclusion.
-A study conducted for New Woman magazine indicates that the number of children desired by newly-married American couples is distributed as follows. 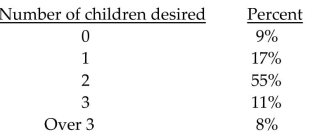
 At the 1% significance level, does it appear that the "number of children desired" distribution of California couples is different from that of the American population as a whole?
At the 1% significance level, does it appear that the "number of children desired" distribution of California couples is different from that of the American population as a whole?
(Essay)
4.8/5  (31)
(31)
Suppose that you wish to perform a chi-square test of independence. Give an example of sample data for which assumption 1 (all expected frequencies are 1 or greater)is violated. You should present the sample data in the form of a contingency table.
(Essay)
4.9/5  (43)
(43)
Perform a chi-square homogeneity test, provided the conditions for the test are met. Use the critical-value approach.
-300 men and 300 women were selected and asked whether they planned to vote in the next election. The results of independent simple random samples are given in the table below, showing the voting intentions by gender. Use a 1% significance level to test the claim that there is a difference in the distribution of voting intentions for men and women. Men Women Plan to vote 170 185 Do not plan to vote 130 115
(Essay)
4.9/5  (43)
(43)
Showing 1 - 20 of 74
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)