Exam 8: Polar Coordinates; Vectors
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Match the graph to one of the polar equations.
-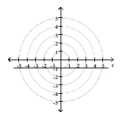 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.7/5  (35)
(35)
Find the requested vector.
-v = -4i - 5j + k, w = -5i + 3j - k Find a vector orthogonal to both v and w.
(Multiple Choice)
4.9/5  (34)
(34)
Find the indicated cross product.
-v = 4i + 2j + 5k, w = -5i + 2j + 4k Find w × v.
(Multiple Choice)
4.9/5  (26)
(26)
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
-
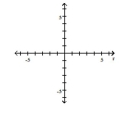 A)
A)
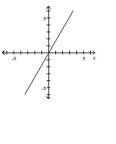 ; line through the pole making
an angle of with the polar axis
B)
; line through the pole making
an angle of with the polar axis
B)
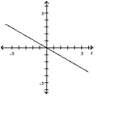 ; line through the pole making
an angle of with the polar axis
C)
; line through the pole making
an angle of with the polar axis
C)
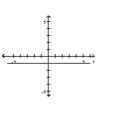 ; horizontal line units
below the pole
D)
; horizontal line units
below the pole
D)
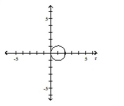 circle, radius
center at in rectangular coordinates
circle, radius
center at in rectangular coordinates
(Multiple Choice)
4.9/5  (38)
(38)
Find all the complex roots. Leave your answers in polar form with the argument in degrees.
-The complex fifth roots of
(Multiple Choice)
4.8/5  (34)
(34)
The letters x and y represent rectangular coordinates. Write the equation using polar coordinates (r, θ).
-
(Multiple Choice)
4.7/5  (28)
(28)
Solve the problem.
-If v = 3i - 5j and w = -7i + 4j, find 3v - 4w.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 261 - 270 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)