Exam 8: Polar Coordinates; Vectors
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Write the complex number in polar form. Express the argument in degrees, rounded to the nearest tenth, if necessary.
-
(Multiple Choice)
4.8/5  (37)
(37)
The rectangular coordinates of a point are given. Find polar coordinates for the point.
-(100, -30) Round the polar coordinates to two decimal places, with θ in degrees.
(Multiple Choice)
4.7/5  (38)
(38)
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
-
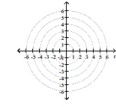 A)
A)
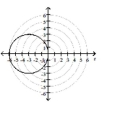 ; circle, radius 3
center in rectangular coordinates
B)
; circle, radius 3
center in rectangular coordinates
B)
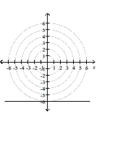 ; horizontal line 6 units
below the pole
C)
; horizontal line 6 units
below the pole
C)
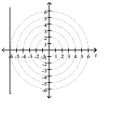 ; vertical line 6 units
to the left of the pole
D)
; vertical line 6 units
to the left of the pole
D)
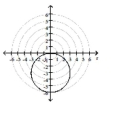 ; circle, radius 3
center at in rectangular coordinates
; circle, radius 3
center at in rectangular coordinates
(Multiple Choice)
5.0/5  (29)
(29)
Find the requested vector.
-v = -3i - 5j + k Find a vector orthogonal to both v and i + j.
(Multiple Choice)
5.0/5  (32)
(32)
State whether the vectors are parallel, orthogonal, or neither.
-
(Multiple Choice)
4.9/5  (31)
(31)
Identify and graph the polar equation.
-
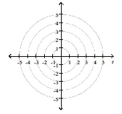 A)
A)
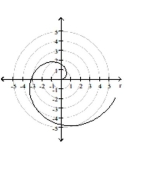 logarithmic spiral
B)
logarithmic spiral
B)
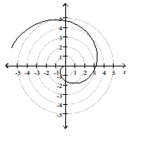 logarithmic spiral
C)
logarithmic spiral
C)
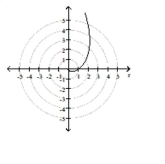 logarithmic spiral
D)
logarithmic spiral
D)
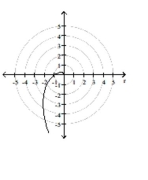 logarithmic spiral
logarithmic spiral
(Multiple Choice)
5.0/5  (32)
(32)
Match the graph to one of the polar equations.
-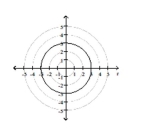 A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.8/5  (37)
(37)
State whether the vectors are parallel, orthogonal, or neither.
-v = 4i + j, w = i - 4j
(Multiple Choice)
4.8/5  (38)
(38)
Test the equation for symmetry with respect to the given axis, line, or pole.
-
(Multiple Choice)
4.9/5  (35)
(35)
Find all the complex roots. Leave your answers in polar form with the argument in degrees.
-The complex fifth roots of
(Multiple Choice)
4.7/5  (30)
(30)
Match the point in polar coordinates with either A, B, C, or D on the graph.
-
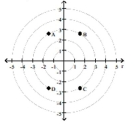
(Multiple Choice)
4.9/5  (40)
(40)
The letters r and θ represent polar coordinates. Write the equation using rectangular coordinates (x, y).
-
(Multiple Choice)
4.8/5  (30)
(30)
Find the angle between v and w. Round your answer to one decimal place, if necessary.
-v = -5i + 7j, w = -6i - 4j
(Multiple Choice)
4.8/5  (28)
(28)
Test the equation for symmetry with respect to the given axis, line, or pole.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-An SUV weighing 4,400 pounds is parked on a street which has an incline of 15°. Find the force required to keep the SUV from rolling down the hill and the force of the SUV perpendicular to the hill. Round the forces to the
Nearest hundredth.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 101 - 120 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)