Exam 6: The Circular Functions and Their Graphs
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Solve the problem.
-Let angle be designated . Angles and VRQ are right angles. If , find the exact length of .
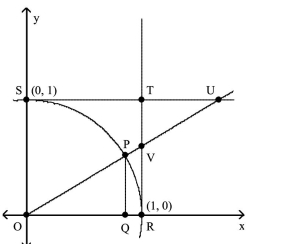
(Multiple Choice)
4.7/5  (39)
(39)
Solve the problem.
-A weight attached to a spring is pulled down 3 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time seconds.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-Determine the length of a pendulum that has a period of 2 seconds.
(Multiple Choice)
4.9/5  (34)
(34)
Find the area of a sector of a circle having radius r and central angle θ. If necessary, express the answer to the nearest
tenth.
-
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-Use regression to find constants , and d so that models the data given below. Round all answers to 9 decimal places.
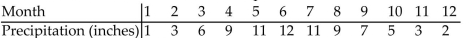
(Multiple Choice)
4.8/5  (37)
(37)
Convert the degree measure to radians. Leave answer as a multiple of π.
-
(Multiple Choice)
4.8/5  (35)
(35)
Find the value of s in the interval [0, π/2] that makes the statement true. Round to four decimal places.
-sec
(Multiple Choice)
4.9/5  (34)
(34)
Convert the radian measure to degrees. Give answer using decimal degrees to the nearest hundredth. Use 3.1416 for π.
-2
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-Let angle be designated . Angles and VRQ are right angles. If , find the exact length of OU.
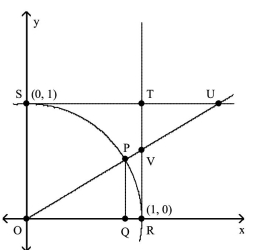
(Multiple Choice)
4.8/5  (32)
(32)
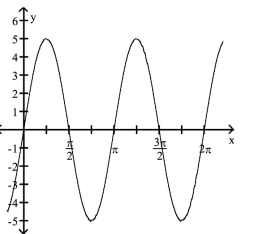
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
(Multiple Choice)
4.7/5  (30)
(30)
Convert the degree measure to radians. Leave answer as a multiple of π.
-
(Multiple Choice)
4.9/5  (42)
(42)
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .
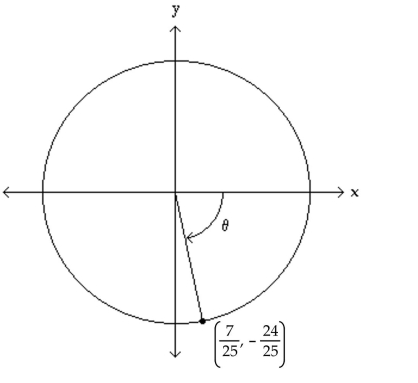
(Multiple Choice)
4.8/5  (37)
(37)
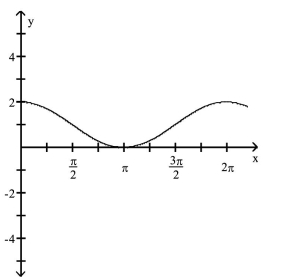
The function graphed is of the form y = cos x + c, y = sin x + c, y = cos(x - d), or y = sin(x - d), where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (36)
(36)
Showing 181 - 200 of 289
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)